cuda_learning_02 内存体系 & reduce优化
cuda_learning_02
内容主要来自知乎文章,CUDA(二):GPU的内存体系及其优化指南,本文是学习笔记。
一、GPU的内存体系
各级内存及其特点
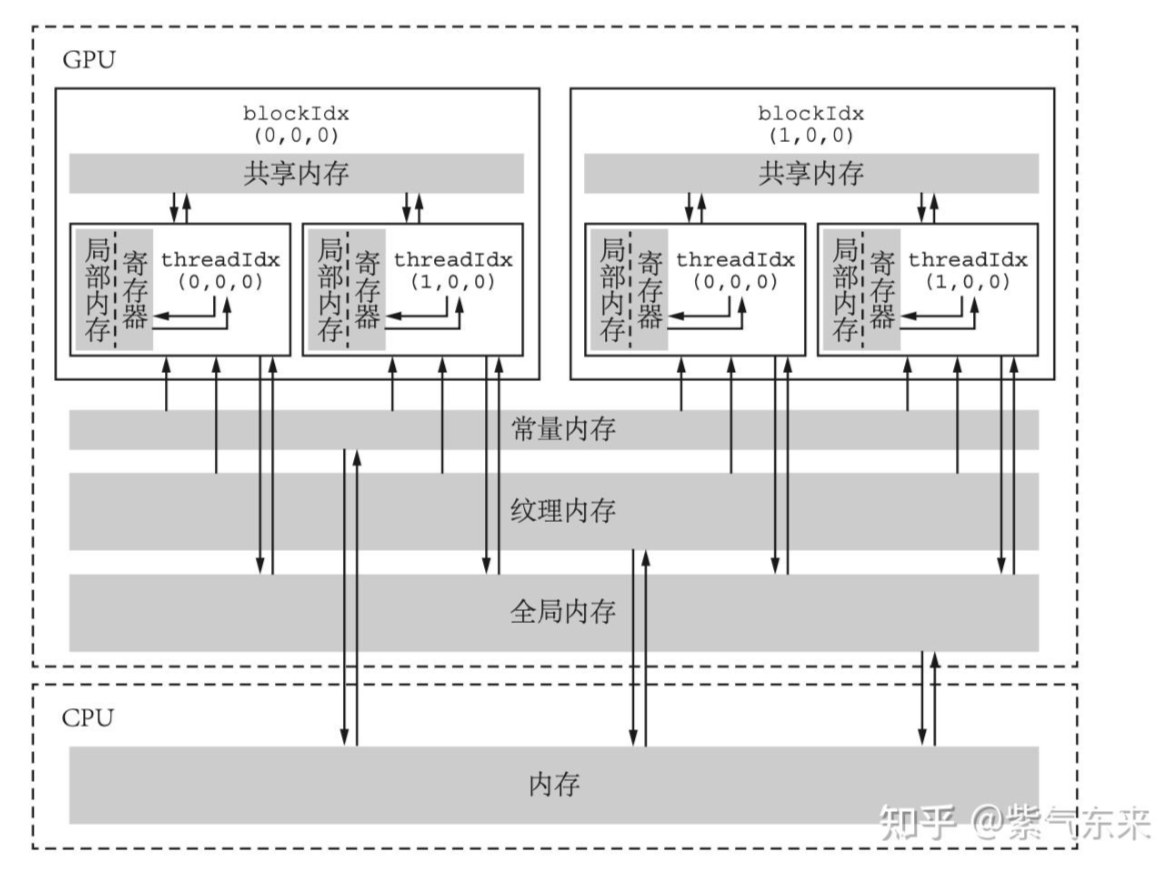
全局内存(global memory)
最大,延迟最高、最长使用的内存,常说的“显存”中的大部分都是全局内存。可以用 cudaMemcpy函数将主机的数据复制到全局内存,或者反过来。
常量内存(constant memory)
常量内存是指存储在片下存储的设备内存,但是通过特殊的常量内存缓存(constant cache)进行缓存读取,常量内存为只读内存。 常量内存数量有限,一共仅有 64 KB,由于有缓存,常量内存的访问速度比全局内存高,但得到高访问速度的前提是一个线程束中的线程(一个线程块中相邻的 32 个线程)要读取相同的常量内存数据。
一个使用常量内存的方法是在核函数外面用 __constant__ 定义变量,并用 API 函数 cudaMemcpyToSymbol 将数据从主机端复制到设备的常量内存后 供核函数使用。
纹理内存(texture memory)和表面内存(surface memory)
纹理内存和表面内存类似于常量内存,也是一 种具有缓存的全局内存,有相同的可见范围和生命周期,而且一般仅可读(表面内存也可 写)。不同的是,纹理内存和表面内存容量更大,而且使用方式和常量内存也不一样。
寄存器(register)
寄存器是线程能独立访问的资源,它所在的位置与局部内存不一样,是在片上(on chip)的存储,用来存储一些线程的暂存数据。寄存器的速度是访问中最快的,但是它的容量较小。
在核函数中定义的不加任何限定符的变量一般来说就存放于寄存器(register)中。 各种内建变量,如 gridDim、blockDim、blockIdx、 threadIdx 及 warpSize 都保存在特殊的寄存器中,以便高效访问。
寄存器变量仅仅被一个线程可见,寄存器的生命周期也与所属线程的生命周期 一致,从定义它开始,到线程消失时结束。
局部内存(local memory)
局部内存和寄存器几乎一 样,核函数中定义的不加任何限定符的变量有可能在寄存器中,也有可能在局部内存中。寄存器中放不下的变量,以及索引值不能在编译时就确定的数组,都有可能放在局部内存中。
虽然称之为“局部内存”,但是其本质是设备全局内存(但不同于全局内存)中为每个线程单独分配的一块内存。所以,局部内存的延迟也很高,每个线程最多能使用高达512 KB的局部内存,但使用过多会降低程序的性能。
共享内存(shared memory)
共享内存和寄存器类似,存在于芯片上,具有仅次于寄存器的读写速度,数量也有限。 一个使用共享内存的变量可以 __shared__ 修饰符来定义。
共享内存对整个线程块可见,其生命周期也与整个线程块一致。共享内存的主要作用是减少对全局内存的访问,或者改善对全局内存的访问模式。

L1和L2 缓存
每个 SM 都有一个 L1 缓存,所有 SM 共享一个 L2 缓存。L1 和 L2 缓存都被用来存储局部内存和全局内存中的数据,也包括寄存器中溢出的部分,以减少延时。
从物理结构上来说,在最新的GPU架构中,L1 缓存、纹理缓存及共享内存三者是统一的。但从编程的角度来看,共享内存是可编程的缓存(共享内存的使用完全由用户操控),而L1 和 L2 缓存是不可编程的缓存(用户最多能引导编译器做一些选择)。
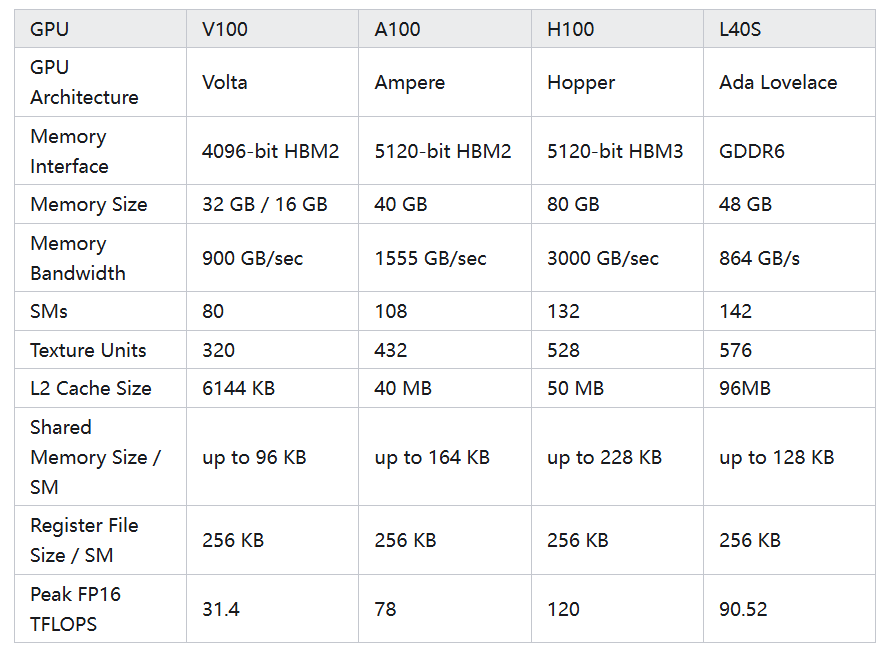
SM 构成及典型GPU的对比
一个 GPU 是由多个 SM 构成的。一个 SM 包含如下资源:
一定数量的寄存器。
一定数量的共享内存。
常量内存的缓存。
纹理和表面内存的缓存。
L1缓存。
线程束调度器(warp scheduler) 。
执行核心,包括:
- 若干整型数运算的核心(INT32) 。
- 若干单精度浮点数运算的核心(FP32) 。
- 若干双精度浮点数运算的核心(FP64) 。
- 若干单精度浮点数超越函数(transcendental functions)的特殊函数单元(Special Function Units,SFUs)。
- 若干混合精度的张量核心(tensor cores)
单精度浮点数超越函数(transcendental functions) 的 特殊函数单元(Special Function Units,SFUs) 是指一种硬件单元,它专门用于执行一些数学上超越(超出普通代数运算)函数的计算,如三角函数(sin, cos),指数函数(exp),对数函数(log),平方根(sqrt)等。
张量核心(Tensor Cores):主要用于加速深度学习中的矩阵运算,尤其是低精度浮点数运算(如 FP16)。
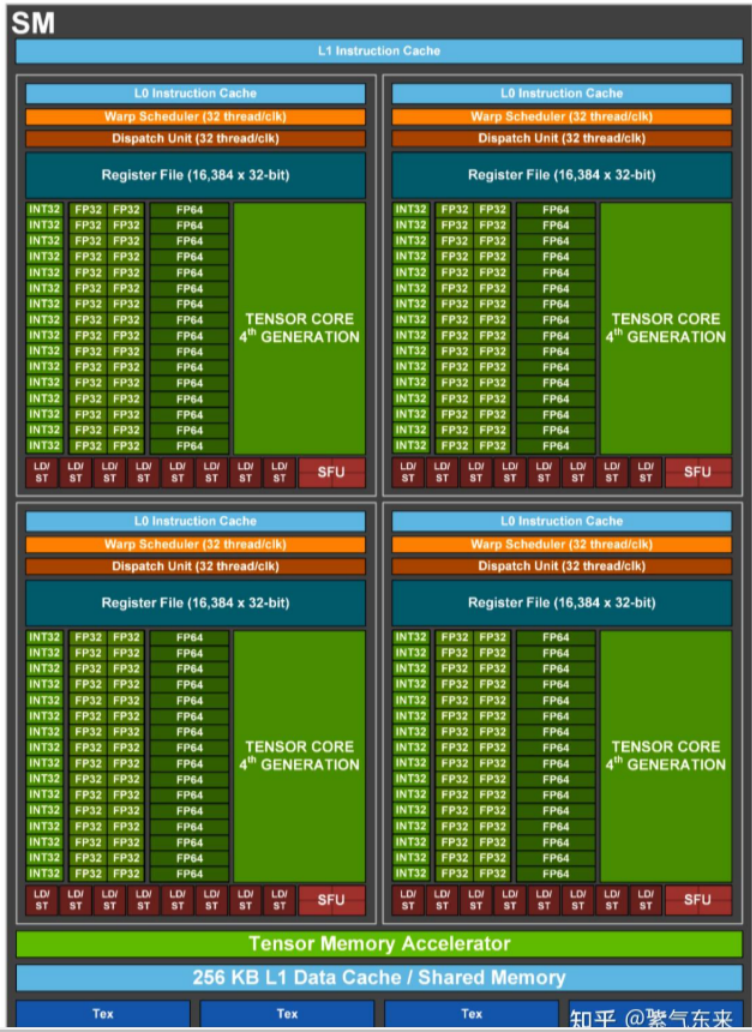
L1 Instruction Cache
用于缓存线程束(warp)的指令,提高指令读取的效率。
Warp Scheduler 和 Dispatch Unit
Warp Scheduler(线程束调度器):
每个 SM 中有多个 Warp Scheduler,每个调度器可以每个时钟周期调度 32 个线程(一个 Warp)。调度线程束执行任务,包括加载指令、分配执行单元等。
Dispatch Unit(指令派发单元):
Warp Scheduler 将指令分配给不同的执行单元(如 FP32、FP64、INT32 核心或 SFUs 等),由 Dispatch Unit 具体派发。
Register File(寄存器文件)
执行核心
L0 Instruction Cache 和数据缓存
L0 Instruction Cache:
每个 Warp Scheduler 附带的更小的指令缓存,用于加速最近使用的指令。
L1 Data Cache / Shared Memory:
每个 SM 配备 256 KB 的共享内存或 L1 数据缓存。
Load/Store 单元
负责从全局内存中加载数据或将计算结果存储到全局内存中。
纹理单元(Tex)
纹理单元专门用于处理纹理数据加载,通常在图形渲染中使用。
Tensor Memory Accelerator
针对张量核心操作的特殊加速器,用于处理张量内存的加载和存储。
GPU 之外:近存计算与存算一体
在GPU的层次结构之外,为了降低访存成本,获得更高的性能,近存计算与存算一体逐渐成为热门的方向。
近存计算: Graphcore IPU
存算一体: 后摩智能 H30
存算一体或者存内计算的核心思想是,通过对存储器单元本身进行算法嵌入,使得计算可以在存储器单元内完成。
二、通过归约(Reduction)操作理解GPU内存体系
关于reduce优化,CUDA(二):GPU的内存体系及其优化指南(blog1)和深入浅出GPU优化系列:reduce优化(blog2)都做出了很详细的讲解,两篇文章都写得非常详细,优化的角度也是大同小异的,下面的内容主要是整理两篇文章中提到优化方向,并对所有提到优化角度做一个小小的总结。
首先,算法reduce即求解$x=x_0 \bigotimes x1 \bigotimes x_2 \bigotimes x_3 \bigotimes … \bigotimes x_n$。其中$\bigotimes$可表示为求sum,min,max,avg等操作,最后获得的输出相比于输入一般维度上会递减。在GPU中,reduce采用了一种树形的计算方式,并且由于GPU没有针对global数据的同步操作,只能针对block的数据进行同步。所以,reduce一般分为两个阶段。
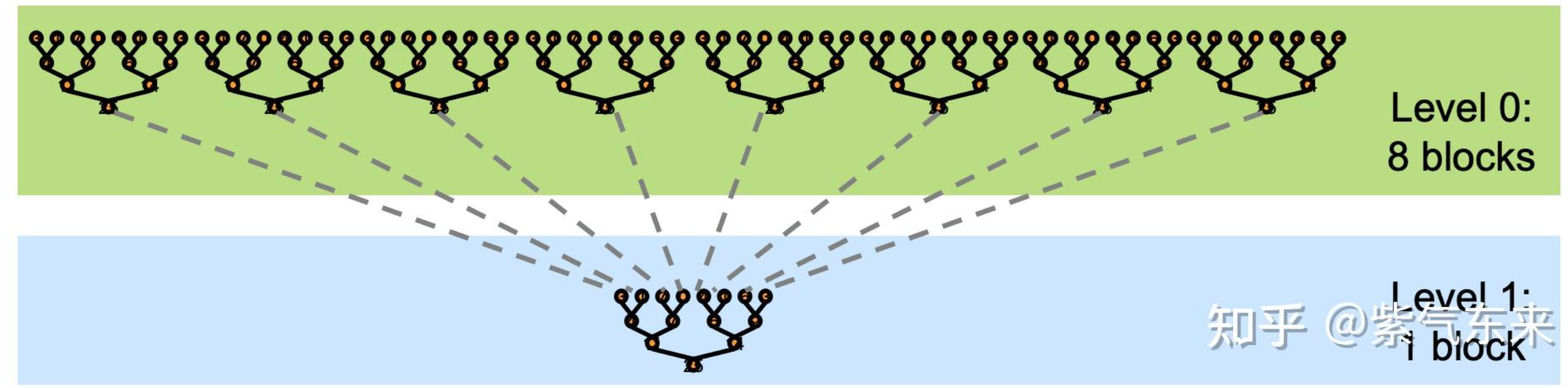
blog1
1. cpu 版本
1 | real reduce(const real *x, const int N) |
1 | sum = 33554432.000000. |
2. 仅使用全局内存
每个线程负责其唯一id对应的那个位置的值的计算,N=1e8,每个线程块有128个线程。
1 | void __global__ reduce_global(real *d_x, real *d_y) |
3. 使用共享内存实现规约
共享内存的带宽远大于全局内存,和上面的代码主要区别如下:
1 | const int tid = threadIdx.x; |
完整代码:
1 | void __global__ reduce_shared(real *d_x, real *d_y) |
使用共享内存相对于仅使用全局内存还有两个好处: 一个是不再要求全局内存数组的长度 N 是线程块大小的整数倍,另一个是在规约的过程中不会改变全局内存数组中的数据(在仅使用全局内存时,数组 d_x 中的部分元素被改变)。
4.使用动态共享内存实现
上边使用共享内存数组时,指定了一个固定的长度(128,即blockDim.x)。 这种静态的方式可能会导致错误的发生,因此有必要使用动态操作。
只需要修改两个地方:
1 | //1.调用核函数的执行配置中写下第三个参数 |
5. 其他优化方法
5.1 原子函数
前面几个版本的归约函数中,内核函数只是将一个较长的数组d_x变成了一个较短的数组d_y,而对后面这个较短数组的归约过程实际上是在cpu上进行的。而在cpu上进行计算花费的时间占总共计算时间的大部分。
所以说如果能在GPU计算出最终的结果,则有望显著地减少整体的计算时间。有两种方法能够在 GPU 中得到最终结果,一是用另一个核函数将较短的数组进一步归约,得到最终结果; 二是在先前的核函数的末尾利用原子函数进行归约,直接得到最终结果。
之前的写法:
1 | if (tid == 0) |
改成:
1 | if (tid == 0) |
但是这个过程是可能出现读写冲突的,所以需要使用原子操作。故实际写法如下:
1 | //atomicAdd(address, val) 待累加变量的地址 address,累加的值 val。 |
5.2 线程束同步、线程束函数
线程束(warp) 是 SM 中基本的执行单元。一个线程束由32个连续线程组成,这些线程按照单指令多线程(SIMT)方式执行。这样如果在条件语句中,同一线程束中的线程执行不同的指令,就会发生线程束分化(warp divergence) ,导致性能出现明显下降。
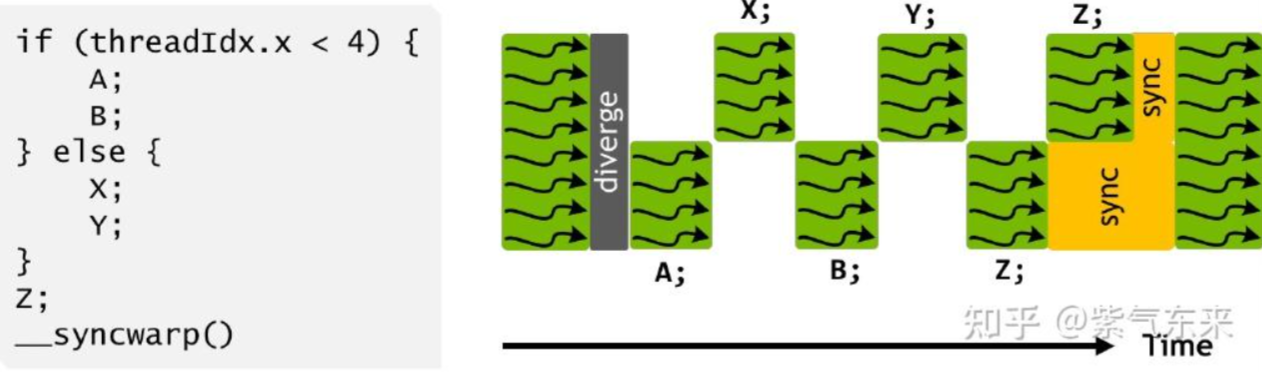
在归约问题中,当所涉及的线程都在一个线程束内时,可以将线程块同步函 数 __syncthreads 换成一个更加廉价的线程束同步函数 __syncwarp。
1 | for (int offset = blockDim.x >> 1; offset >= 32; offset >>= 1) |
另外还可以利用线程束洗牌函数进行归约计算,函数 __shfl_down_sync 的作用是将高线程号的数据平移到低线程号中。__shfl_down_sync 是 warp 级别的操作,硬件支持非常高效,不依赖共享内存,依赖于寄存器操作。
1 | for (int offset = 16; offset > 0; offset >>= 1) |
相比之前的版本,有两处不同。第一,使用速度更快的寄存器而不是共享内存。第二,去掉了束同步函数,这是因为洗牌函数能够自动处理同步与读-写竞争问题。
5.3 协作组
协作组(cooperative groups)可以看作是线程块和线程束同步机制的推广,它提供了更为灵活的线程协作方式,包括线程块内部的同步与协作、线程块之间的(网格级的)同步与协作及设备之间的同步与协作。
使用协作组的功能时需要在相关源文件包含如下头文件 ,并导入命名空间:
1 |
|
可以用函数 tiled_partition 将一个线程块划分为若干片(tile),每一片构成一个 新的线程组。目前仅仅可以将片的大小设置为 2 的正整数次方且不大于 32。例如,如下语句通过函 数 tiled_partition 将一个线程块分割为我们熟知的线程束:
1 | thread_group g32 = tiled_partition(this_thread_block(), 32); |
同时线程块片类型中也有洗牌函数,可以利用线程块片来进行数组归约的计算。
1 | real y = s_y[tid]; |
5.4 解决idle线程
在前边的例子中, 我们都使用大小为 128 的线程块,所以当 offset 等于 64 时,只用了 1/2 的线程进行计算,其余线程闲置。当 offset 等于 32 时,只用了 1/4 的线程进行计算,其余线程闲置。最终,当 offset 等于 1 时,只用了 1/128 的线程进行计算,其余线程闲置。归约过程一共用了 log2 128 = 7 步, 故归约过程中线程的平均利用率只有 (1/2 + 1/4 + …)/7 ≈ 1/7 。
为了提高效率,可以考虑在归约之前将多个全局内存数组的数据累加到一个共享内存数组的一个元素中。 用一个寄存器变量 y,用来在循环 体中对读取的全局内存数据进行累加, 在规约之前,必须将寄存器中的数据复制到共享内存。(简单来说,就是增加每个线程的计算任务,减少线程总数)
1 | real y = 0.0; |
执行配置设置为<<<10240,128>>>,完整代码如下:
1 | void __global__ reduce_idle(const real *d_x, real *d_y, const int N) |
10240*128=1310720,100000000/1310720=76。即每个线程会先计算至少76个数字的和,再执行类似上述的操作。
5.5 静态全局内存
在之前的 reduce 函数中,需要为数组 d_x 分配与释放设备内存。实际上,设备内存的分配与释放是比较耗时的。一种优化方案是使用静态全局内存代替这里的动态全局内存。简单来说其实就是代码1比代码2更快。
1 | // 1 |
利用函数 cudaGetSymbolAddress 将该指针与静态全局变量 static_x 联系起来。
1 | __device__ real static_x[N]; //定义在全局 |
这个方法其实存在一定的局限性,在实际应用中也许数据从cpu到gpu这个过程都是在python代码实现了,导致这个方法无法应用。
6. 总结
总结一下整个优化流程。首先是最基本的使用共享内存,关于静态共享内存还是动态共享内存,我认为这个区别并不是很大,但是通常是使用动态共享内存。这是泛用性较高、性能提升较大的一个点。
在这之后存在的问题是可以将长数组归约成短数组(长度等于调用的线程块数),但是依旧没有获得最终答案,此时,如果在cpu计算短数组的话,那么$time_{cpu} >> time_{gpu}$。为解决这个问题,有两个方法,一是再调一个线程块;二是使用原子操作,每个线程块算完直接写到最后的答案中,而这个过程会存在读写冲突,所以需要使用原子操作。当然原子操作这个技巧在其他问题中也许无法应用,泛用性可能较低,不过在这个问题中带来的性能提升较大。
之后,为了解决可能存在的线程束分化的问题,使用线程束同步、线程束函数、协作组等方法,充分利用SIMD的特性,充分利用寄存器的带宽实现优化。解决线程束分化应该是一个比较重要的点,泛用性较高,带来的性能提升也较大。不过,如果程序本身不存在线程束分化,那么仅仅使用线程束函数、协作组的话带来的提升可能有限。再者需要解决的问题也不一定有适配的线程束函数。
再者,就是发现线程工作不均衡,有的线程的计算量很小,即idle线程,为了解决这一问题,常见的做法就是增加每个线程的工作量(原本繁忙的线程增加的相对少,而idle的线程增加的多),提高线程利用率。这也是一个性能提升较大,泛用性较高的技巧。
最后,就是关于静态全局内存。作为一名acmer,开数组的时候都是
1 | int maxn = 1e5 + 5; |
而不是
1 | int main() |
静态全局内存的优化思路跟上面的做法类似,个人认为对性能的提升是有的,但是泛用性较低。
最后,附上原作者的实验结果,作为重要参考。
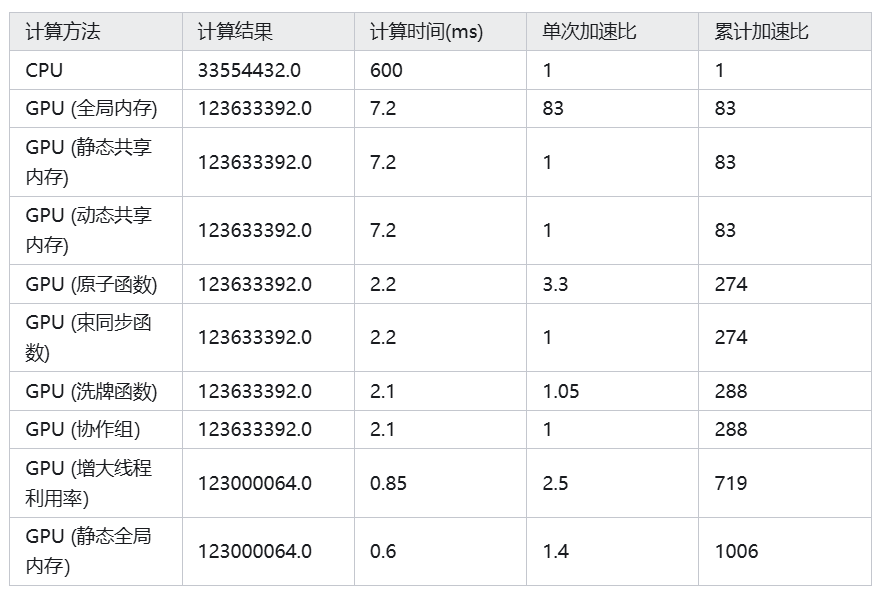
blog2
这篇博客中多次提到如下参数:
BlockNum:即开启的block数量,即上面所说的M,代表需要将数组切分为几份。
Thread_per_block:每个block中开启的线程数,一般而言,取128,256,512,1024这几个参数会比较多。
Num_per_block:每个block需要进行reduce操作的长度。
Baseline算法
基准算法,没什么特别的,但是提到了一些观点。首先,说是优化的本质是通过软件榨干硬件资源,所以必须清楚地了解代码在硬件上的执行过程才能更好地进行优化。
从硬件角度来分析一下代码。为了执行代码,GPU需要分配两种资源,一个是存储资源,一个是计算资源。存储资源包括在global memory、shared memory等存储空间。需要注意的是,shared memory存在bank冲突的问题,因而需要格外小心。 计算资源其实是根据thread数量来确定的,一个block中分配256个thread线程,32个线程为一组,绑定在一个SIMD单元。256个线程可以简单地理解为分配了8组SIMD单元。(但实际的硬件资源分配不是这样,因为一个SM的计算资源有限,不可能真的给每一个block都分配这么多的SIMD单元。)
优化技巧1:解决warp divergence
emmm,这篇里的offset从小到大枚举的,上一篇是从大到小枚举的,线程束分化问题比较严重,改成上一篇的枚举顺序其实就好了。
优化技巧2:解决bank冲突
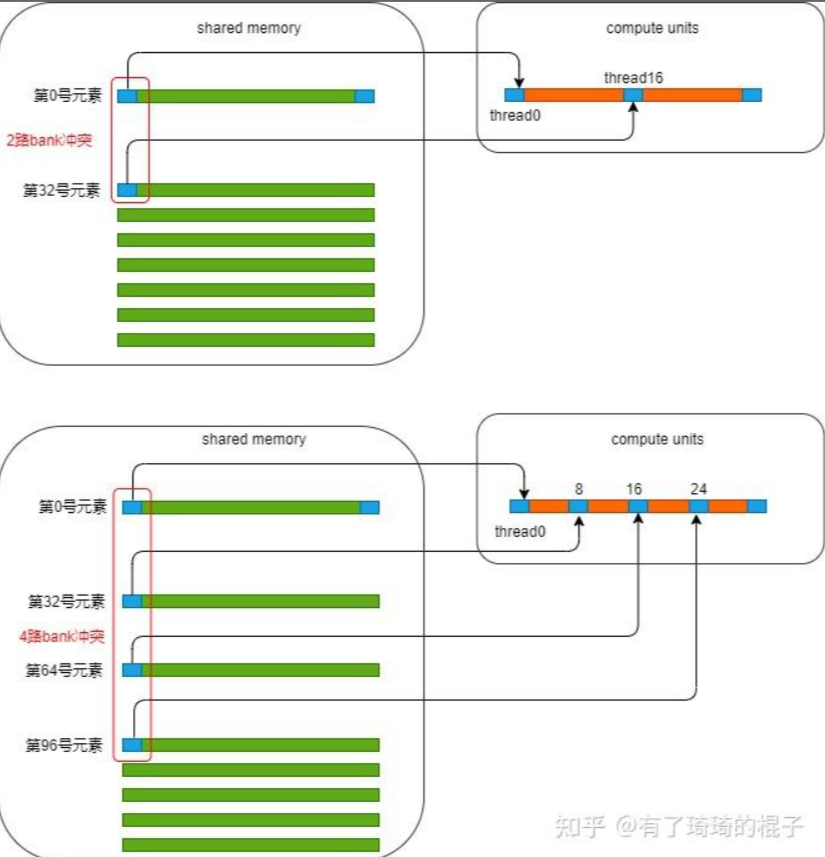
首先,什么是bank冲突?可以理解为seme跟线程束一样也是以32为单位,如上图,一行32个元素,而1列是一个bank,每个bank能够并行处理访问请求,但如果多个线程试图访问相同的bank,就会发生冲突,影响性能。
这篇里的offset从小到大枚举的,确实是会出现bank冲突的,第一次迭代会出现2路bank冲突,第二次迭代会出现4路bank冲突,以此类推。。。
解决方法就是,offset从大到小枚举。
优化技巧3:解决idle线程
方法是将Num_per_block增加一倍。也就是说原来一个block只需要管256个数就行,现在得管512个数了。与blog1中方法类似。
优化技巧4:展开最后一维减少同步
存在的问题是多余的线程同步,到最后几轮迭代时,此时的block中只有warp0在干活(blog1中的线程束同步)。
而这32个线程又是在一个SIMD单元上,存在天然的同步,所以可以把最后一维展开减少同步(循环展开)。
1 | __device__ void warpReduce(volatile float* cache,int tid){ |
优化技巧5:完全展开减少计算
把for循环完全展开,变成一堆if语句,个人感觉带来的提升是有限的,并且GPU硬件架构的不断发展,NV在编译器上面也做了较多的工作,并且这个优化纯纯是折磨开发者,好好的for循环不写,去写一堆if。
优化技巧6:合理设置block数量
引用一下原文:如果一个线程被分配更多的work时,可能会更好地覆盖延时。这一点比较好理解。如果线程有更多的work时,对于编译器而言,就可能有更多的机会对相关指令进行重排,从而去覆盖访存时的巨大延时。虽然这句话并没有很好地说明在某种程度上而言,block少一些会更好。但是,有一点不可否认,block需要进行合理地设置。理论上,block取SM数量的倍数会比较合理。
优化技巧7:使用shuffle指令
Shuffle指令是一组针对warp的指令。Shuffle指令最重要的特性就是warp内的寄存器可以相互访问。
总结
优化方法和角度和blog1中的大同小异,比较新的一个角度就是解决bank冲突,这是一个对性能提升较大,泛用性较高的方法。其他的类似展开循环、合理设置block数量,相对没那么重要(个人感觉)。
贴一下原作者的性能对比图。
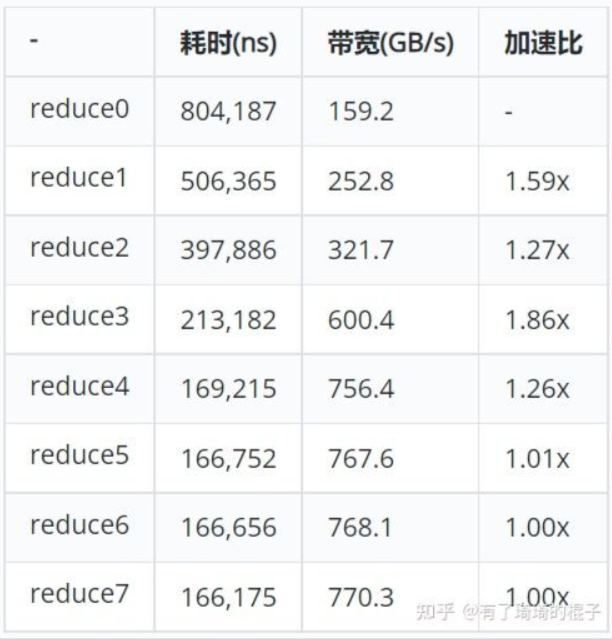
最后的最后
代码仓库:神秘链接。
性能对比:
| 计算方法 | 计算时间(ms) | 单次加速比 | 累计加速比 |
|---|---|---|---|
| CPU | 195.956955 | 1 | 1 |
| 全局内存 | 1.8026 | 108.70 | 108.70 |
| 静态共享内存 | 1.8906 | 0.95 | 103.65 |
| 动态共享内存 | 1.8957 | 1.00 | 103.37 |
| 原子函数 | 1.8735 | 1.01 | 104.59 |
| 线程束同步函数 | 1.5082 | 1.24 | 129.93 |
| 洗牌函数 | 1.6358 | 0.92 | 119.79 |
| 协作组 | 1.6705 | 0.98 | 117.30 |
| 增大线程利用率 | 0.68647 | 2.43 | 285.46 |
实验设备是2080ti,有一说一,这个结果我是不满意的,有的单次加速比<1,可能是设备的问题?还是我的代码的问题?等我有时间一定找出问题所在,一定说是。
Update
回看reduce这部分,虽然写了很多版本的优化,但感觉很多版本的代码意义不大,主要是学习一个优化思路,最近重写了一份新的reduce代码,主要用了 warp shuffle 和 float4,向量化访存其实就可以提高线程利用率,性能接近之前的最佳版本(略优于)。
1 | template<int blockSize> |