cuda_learning_03

发表于 更新于 分类于

cuda_learning_03

1、前置知识
2、Sgemm
3、Hgemm

1. 前置知识

1.1.硬件基础

1.1.1 算计

 查询网站：https://www.techpowerup.com/gpu-specs/

image-20250630221616375

1.1.2 带宽

image-20250630222331096

1.2 Warp divergence

  三元表达式不会造成线程束分化说是。

1.3 异步复制

  可以认为是一种访存方式，指的是__pipeline_memcpy_async()。好处是不使用中间寄存器有助于减少寄存器压力，并可能增加内核占用率。

image-20250630223128730

  但是感觉完全可以被cp.async这个ptx指令代替，或者说两者本质是一个东西。后续只会用到cp.async。

1.4 具体问题

  $C = αAB + βC$

  其中，A的形状是[M, K],B的形状是[K, N],C的形状是[M,N]。为了方便，通常取α = 1，β = 0。

2. Sgemm

  Sgemm的优化，包括4个版本的代码和简要分析，具体分析涉及很多详细的计算分析见Reference。

2.1 CPU实现和naiveSgemm

1
2
3
4
5
6
7
8
9
10
11
12
13
// cpu 实现
void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K)
{
    for (int m = 0; m < M; ++m) 
    {
        for (int n = 0; n < N; ++n) 
        {
            float psum = 0.0;
            for (int k = 0; k < K; ++k) psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
            c[OFFSET(m, n, N)] = psum;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 朴素的 GPU 实现
//__restrict__ 的作用:开发者向编译器保证：在该指针的作用域内，所有通过该指针访问的内存不会通过其他指针或引用被修改。编译器可以据此假设无别名冲突，从而生成更高效的代码。
__global__ void naiveSgemm(float* __restrict__ a, float* __restrict__ b, float* __restrict__ c, const int M, const int K, const int N)
{
    int tidx = blockIdx.x * blockDim.x + threadIdx.x;
    int tidy = blockIdx.y * blockDim.y + threadIdx.y;

    if(tidx < N && tidy < M)
    {
        float sum = 0.0;
        #pragma unroll 
        for(int k = 0; k < K; ++k) sum += a[OFFSET(tidy, k, K)] * b[OFFSET(k, tidx, N)];
        c[OFFSET(tidx, tidy, N)] = sum;
    }
}

  NVIDIA GeForce RTX 3090的执行结果如下，理论算力$FP32 (TFLOPS)=CUDA 核心数 × 加速频率 × 2$，计算得10,496×1.70×2=35.7 TFLOPS。该方法算力利用率仅有4.5%。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
M N K =    128    128   1024, Time =   0.00008499   0.00008908   0.00009715 s, AVG Performance =   376.6978 Gflops
M N K =    192    192   1024, Time =   0.00008909   0.00009093   0.00009216 s, AVG Performance =   830.2995 Gflops
M N K =    256    256   1024, Time =   0.00008909   0.00008970   0.00009114 s, AVG Performance =  1496.2557 Gflops
M N K =    384    384   1024, Time =   0.00016486   0.00017285   0.00017510 s, AVG Performance =  1747.1090 Gflops
M N K =    512    512   1024, Time =   0.00031949   0.00032122   0.00032973 s, AVG Performance =  1671.3371 Gflops
M N K =    768    768   1024, Time =   0.00063898   0.00065208   0.00065434 s, AVG Performance =  1852.4714 Gflops
M N K =   1024   1024   1024, Time =   0.00106189   0.00106394   0.00106598 s, AVG Performance =  2018.4210 Gflops
M N K =   1536   1536   1024, Time =   0.00281805   0.00282910   0.00284774 s, AVG Performance =  1707.9060 Gflops
M N K =   2048   2048   1024, Time =   0.00560026   0.00560722   0.00561152 s, AVG Performance =  1531.9420 Gflops
M N K =   3072   3072   1024, Time =   0.01216819   0.01321758   0.01334579 s, AVG Performance =  1462.2455 Gflops
M N K =   4096   4096   1024, Time =   0.02087629   0.02089912   0.02097050 s, AVG Performance =  1644.0758 Gflops
M N K =   6144   6144   1024, Time =   0.04926976   0.04949125   0.04952781 s, AVG Performance =  1562.0824 Gflops
M N K =   8192   8192   1024, Time =   0.08597197   0.08599675   0.08600986 s, AVG Performance =  1598.1878 Gflops
M N K =  12288  12288   1024, Time =   0.19243827   0.19409776   0.19477504 s, AVG Performance =  1593.2056 Gflops
M N K =  16384  16384   1024, Time =   0.34301132   0.34313369   0.34316391 s, AVG Performance =  1602.1622 Gflops

  这个方法的计算访存比非常低，并且存在大量冗余的全局内存访问。

2.2 矩阵分块并利用Shared Memory和Registers（v1）

  上面提到了naiveSgemm的问题，GPU对Shared Memory和Registers是高于Global Memory的，所以可以利用Shared Memory和Registers作为一个类似于cache的效果，并提高计算访存比，这是一个容易想到的角度，具体要如何做，接下来简要说明。

image-20250630225728596

  核心目标可以认为是提高计算访存比，具体矩阵分块如上图（图片来源）。下面详细分析一下线程块等具体的大小选择。

  对于每一个分块：

  计算量：$BM \times BN \times K \times 2$

  访存量：$(BM + BN) \times K \times 4 Byte$

  计算访存比：$\frac{BM \times BN}{2(BM + BN)} = \frac{1}{2(\frac{1}{BN} + \frac{1}{BM})}$

  由上式可知BM和BN越大，计算访存比越高，性能就会越好。但是由于 Shared Memory 容量的限制(3090 1个SM大致96KB)，而一个Block需要占用 $BK \times (BM + BN) \times 4 Bytes$大小。

  TM和TN的取值也受到两方面限制，一方面是线程数的限制，一个Block中有$\frac{BM}{TM} \times \frac{BN}{TN}$个线程，这个数字不能超过1024，且不能太高防止影响SM内Block间的并行；另一方面是寄存器数目的限制，一个线程至少需要TM * TN个寄存器用于存放矩阵 C 的部分和，再加上一些其它的寄存器，所有的寄存器数目不能超过256，且不能太高防止影响SM内同时并行的线程数目。

  最终选取 BM = BN = 128，BK = 8，TM = TN = 8，则此时计算访存比为32。3090的理论算力35.7TFLOPS，理论带宽是936.2 GB/s。不过实测算力在30TFLOPS左右，实测带宽在789GB/s左右，所以我认为应该以这两个数据为标准。此时 30TFLOPS/32 = 938GB/s，带宽多少还是会限制计算性能，但已经好很多了。

  关于为什么沿着k维度切成更小的bk，而不是A沿m切，B沿n切？

  因为这样切可以保证每个小A分块和小B分块只会加载一次。

  按理说有一个中间优化，就是其他不变，但是每个线程还是只计算一个元素，而不是Tm * Tn。一个线程计算Tm * Tn个原因是：可以减少对shared memory的访存量。

  其实这一步的优化除了提高了计算访存比，使用更快的Shared Memory和Registers，还有涉及到提高硬件利用率的角度（原本一个线程计算一个数据，现在计算Tm * Tn个，即中间优化提到的）。

  根据以上分析，kernel函数实现主要包括以下步骤：

  • 从Global Memory加载对应的矩阵分块到Shared Memory中。

      每个线程刚好负责A矩阵的4个元素和B矩阵的4个元素，刚好可以用FLOAT4来操作，分配好每个线程负责的元素即可。

  • 计算对应的C矩阵

  • 写回Global Memory

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
// 矩阵分块、Shared Memory、Registers
__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c, const int M, const int K, const int N)
{
    const int BM = 128;
    const int BN = 128;
    const int BK = 8;
    const int TM = 8;
    const int TN = 8;
    
    const int bx = blockIdx.x;
    const int by = blockIdx.y;
    const int tx = threadIdx.x;
    const int ty = threadIdx.y;
    const int tid = ty * blockDim.x + tx;

    __shared__ float s_a[BM][BK];
    __shared__ float s_b[BK][BN];

    float r_c[TM][TN] = {0.0};

    // 加载 到 s_a 的 m 行
    int load_a_smem_m = tid >> 1;
    int load_a_smem_k = (tid & 1) << 2;
    int load_b_smem_k = tid >> 5;
    int load_b_smem_n = (tid & 31) << 2;

    // 从 g_a 的 m 行 加载
    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    int cnt = (K + BK - 1) / BK;
    for(int bk = 0; i < cnt; ++bk)
    {
        int load_a_gmem_k = bk * BK + load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        FLOAT4(s_a[load_a_smem_m][load_a_smem_k]) = FLOAT4(a[load_a_gmem_addr]);
        int load_b_gmem_k = bk * BK + load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr]);

        __syncthreads();

        #pragma unroll
        for(int k = 0; k < BK; ++k)
        {
            #pragma unroll
            for(int m = 0; m < TM; ++m)
            {
                #pragma unroll
                for(int n = 0; n < TN; ++n)
                {
                    int comp_a_smem_m = ty * TM + m;
                    int comp_b_smem_n = tx * TN + n;
                    r_c[m][n] += s_a[comp_a_smem_m][k] * s_b[k][comp_b_smem_n];
                }
            }
        }

        __syncthreads();
    }

    #pragma unroll
    for(int i = 0; i < TM; ++i)
    {
        int store_c_gmem_m = by * BM + ty * TM + i;
        #pragma unroll
        for(int j = 0; j < TN; j += 4)
        {
            int store_c_gmem_n = bx * BN + tx * TN + j;
            int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
            FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][j]);
        }
    }
}

  计算结果如下,性能达到了理论峰值的54.5%,达到了实际可达峰值的63.3%：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
M N K =    128    128   1024, Time =   0.00019149   0.00019769   0.00020950 s, AVG Performance =   169.7357 Gflops
M N K =    192    192   1024, Time =   0.00019354   0.00019711   0.00019968 s, AVG Performance =   383.0212 Gflops
M N K =    256    256   1024, Time =   0.00019866   0.00019927   0.00019968 s, AVG Performance =   673.5457 Gflops
M N K =    384    384   1024, Time =   0.00019763   0.00020429   0.00020685 s, AVG Performance =  1478.2557 Gflops
M N K =    512    512   1024, Time =   0.00020480   0.00020531   0.00020582 s, AVG Performance =  2614.9028 Gflops
M N K =    768    768   1024, Time =   0.00020579   0.00020695   0.00020787 s, AVG Performance =  5837.0423 Gflops
M N K =   1024   1024   1024, Time =   0.00020787   0.00020920   0.00020992 s, AVG Performance = 10265.0610 Gflops
M N K =   1536   1536   1024, Time =   0.00034406   0.00034447   0.00034509 s, AVG Performance = 14026.7298 Gflops
M N K =   2048   2048   1024, Time =   0.00065843   0.00065996   0.00066150 s, AVG Performance = 13015.7464 Gflops
M N K =   3072   3072   1024, Time =   0.00129741   0.00130109   0.00130253 s, AVG Performance = 14854.6887 Gflops
M N K =   4096   4096   1024, Time =   0.00208794   0.00208978   0.00209408 s, AVG Performance = 16441.8282 Gflops
M N K =   6144   6144   1024, Time =   0.00461210   0.00461885   0.00462234 s, AVG Performance = 16737.7892 Gflops
M N K =   8192   8192   1024, Time =   0.00686694   0.00707564   0.00795443 s, AVG Performance = 19424.2566 Gflops
M N K =  12288  12288   1024, Time =   0.01572765   0.01590118   0.01641571 s, AVG Performance = 19447.4602 Gflops
M N K =  16384  16384   1024, Time =   0.02786099   0.02943130   0.03024384 s, AVG Performance = 18679.2936 Gflops

2.3 解决 Bank Conflict 问题（v2）

2.3.1 LDS.32

  假设一个warp现在被调度了，它的32个thread此刻要去SMEM上读数。warp发送了一个LDS.32的指令（意思是让所有的thread都取1个数，其大小为4byte，换算成bit就是32）。此时，在cuda的运算中有如下规定：

  • 一个warp发送1次取数指令（不一定是LDS.32），它最多只能从SMEM上读取128bytes（32个数）的数据。这是每个warp发送1次取数指令的能取到的数据量上限。
  • 如果每个thread要取的数，来自不同的bank，我们就认为没有bank conflict。warp发送1次指令，所有的threads即可取回自己想要的数据。
  • 来自同一个bank，但是是这个bank上的同一个数（同一个bank的相同地址，或者说是相同layer），此时也没有bank conflict（广播机制），也是1次指令。
  • 如果某些threads要取的数，来自同一个bank，并且是这个bank上的不同数（同一个bank的不同地址，即不同layer），此时发生了bank conflict。同个warp内的threads想要访问同一个bank下的n个不同的地址，就发生了n-way bank conflict（n头bank conflict）。本该1次指令取回的数，就需要串行发送n次指令。

2.3.2 为什么要对SMEM做bank划分

  简单来说，为了均衡banks的路宽，为了warp间尽量并行，不要相互阻碍。

2.3.3 LDS.64和LDS.128

  LDS.64指令:一次取8bytes的数，即连续的2个数。

  LDS.128指令:一次取16bytes的数，即连续的2个数。

  以LDS.128为例，一个warp需要取128个数，超过了warp单次memory transaction允许的取数上限。所以该warp会把取数过程拆成4个串行的phase（即4次串行的memory transcation）：即0～7，8～15，16～23，24～31。这时bank conflict被定义在每个phase（也就是1/4个warp之内）。

  接下来，我们分析v1中是否存在bank冲突。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int k = 0; k < BK; ++k)
{
    #pragma unroll
    for(int m = 0; m < TM; ++m)
    {
        #pragma unroll
        for(int n = 0; n < TN; ++n)
        {
            int comp_a_smem_m = ty * TM + m;
            int comp_b_smem_n = tx * TN + n;
            r_c[m][n] += s_a[comp_a_smem_m][k] * s_b[k][comp_b_smem_n];
        }
    }
}

  一个简单且不太严谨的对s_b的访问分析，每个线程需要访问s_b的连续8个元素。那么tid = 0的线程，访问bank_id 为 0，1，2，3，4，5，6，7；tid = 1的线程，访问bank_id 为 8，9，10，11，12，13，14，15；这样的话，就会发现tid = 0和tid = 4的线程访问的bank正好相同，所以存在一个8路bank conflict。

  如果使用FLOAT4，你会发现对s_b的访问存在2路bank conflict，解决方法是把每个线程负责的计算的元素修改一下，让每个线程读取两次连续的4个数，而不是连续的8个数。以上面的图片为例，V1中每个线程块负责计算128*128的子矩阵，每个线程负责计算8*8的子矩阵，线程块大小是16*16。V2中每个线程负责4个4*4的子矩阵，即把128*128的子矩阵分成4个64*64的子矩阵(左上、右上、左下、右下)，每个线程负责的那4个4*4子矩阵在这4个64*64的子矩阵的对应位置。

  对于s_a的访问，v1中不存在bank conflict，因为触发了广播机制。但是v1中的访问方式无法使用FLOAT4，因为对s_a的访问是不连续的，解决办法是转置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
// 解决 bank conflict
__global__ void sgemm_V2(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c, const int M, const int N, const int K)
{
    const int bx = blockIdx.x;
    const int by = blockIdx.y;
    const int tx = threadIdx.x;
    const int ty = threadIdx.y;
    const int tid = ty * blockDim.x + tx;

    __shared__ float s_a[BK][BM];
    __shared__ float s_b[BK][BN];

    float r_c[TN][TN] = {0.0};
    float r_load_a[4];
    float r_load_b[4];
    float r_comp_a[TM];
    float r_comp_b[TN];

    int load_a_smem_m = tid >> 1;
    int load_a_smem_k = (tid & 1) << 2;
    int load_b_smem_k = tid >> 5;
    int load_b_smem_n = (tid & 31) << 2;

    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    int cnt = (K + BK - 1) / BK;
    for(int bk = 0; bk < cnt; ++bk)
    {
        int load_a_gmem_k = bk * BK + load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        int load_b_gmem_k = bk * BK + load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);

        s_a[load_a_smem_k][load_a_smem_m] = r_load_a[0];
        s_a[load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
        s_a[load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
        s_a[load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
        FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);

        __syncthreads();

        #pragma unroll
        for(int k = 0; k < BK; ++k)
        {
            FLOAT4(r_comp_a[0]) = FLOAT4(s_a[k][ty * TM / 2]);
            FLOAT4(r_comp_a[4]) = FLOAT4(s_a[k][ty * TM / 2 + BM / 2]);
            FLOAT4(r_comp_b[0]) = FLOAT4(s_b[k][tx * TN / 2]);
            FLOAT4(r_comp_b[4]) = FLOAT4(s_b[k][tx * TN / 2 + BN / 2]);

            #pragma unroll
            for(int m = 0; m < TM; ++m)
            {
                #pragma unroll
                for(int n = 0; n < TN; ++n) r_c[m][n] += r_comp_a[m] * r_comp_b[n];
            }
        }

        __syncthreads();
    }

    #pragma unroll
    for(int i = 0; i < TM / 2; ++i)
    {
        int store_c_gmem_m = by * BM + ty * TM / 2 + i;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i][4]);
    }
    #pragma unroll
    for(int i = 0; i < TM / 2; ++i)
    {
        int store_c_gmem_m = by * BM + ty * TM / 2 + i + BM / 2;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i + TM / 2][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i + TM / 2][4]);
    }

}

  计算结果如下,性能达到了理论峰值的68.6%，达到了实际可达峰值的80%：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
M N K =    128    128   1024, Time =   0.00017306   0.00017603   0.00017715 s, AVG Performance =   190.6225 Gflops
M N K =    192    192   1024, Time =   0.00014438   0.00015247   0.00016486 s, AVG Performance =   495.1511 Gflops
M N K =    256    256   1024, Time =   0.00014438   0.00014479   0.00014541 s, AVG Performance =   926.9590 Gflops
M N K =    384    384   1024, Time =   0.00014541   0.00015677   0.00016179 s, AVG Performance =  1926.3098 Gflops
M N K =    512    512   1024, Time =   0.00015258   0.00015421   0.00015872 s, AVG Performance =  3481.3280 Gflops
M N K =    768    768   1024, Time =   0.00015462   0.00015954   0.00016077 s, AVG Performance =  7571.5533 Gflops
M N K =   1024   1024   1024, Time =   0.00015770   0.00016025   0.00016278 s, AVG Performance = 13400.6000 Gflops
M N K =   1536   1536   1024, Time =   0.00024166   0.00024380   0.00024678 s, AVG Performance = 19819.2506 Gflops
M N K =   2048   2048   1024, Time =   0.00046899   0.00047144   0.00047411 s, AVG Performance = 18220.6316 Gflops
M N K =   3072   3072   1024, Time =   0.00092467   0.00093071   0.00093798 s, AVG Performance = 20766.1658 Gflops
M N K =   4096   4096   1024, Time =   0.00149402   0.00150313   0.00152064 s, AVG Performance = 22858.7997 Gflops
M N K =   6144   6144   1024, Time =   0.00325222   0.00327711   0.00329728 s, AVG Performance = 23590.7485 Gflops
M N K =   8192   8192   1024, Time =   0.00568320   0.00570696   0.00574771 s, AVG Performance = 24082.7044 Gflops
M N K =  12288  12288   1024, Time =   0.01249382   0.01263268   0.01291366 s, AVG Performance = 24479.1828 Gflops
M N K =  16384  16384   1024, Time =   0.02226381   0.02418770   0.02583859 s, AVG Performance = 22728.7352 Gflops

2.4 流水并行化：Double Buffering（v3）

  之前的方法存在 访存-计算 的串行模式流水线，这个方法就是提高访存和计算的并行程度，下图很形象，图片来源。

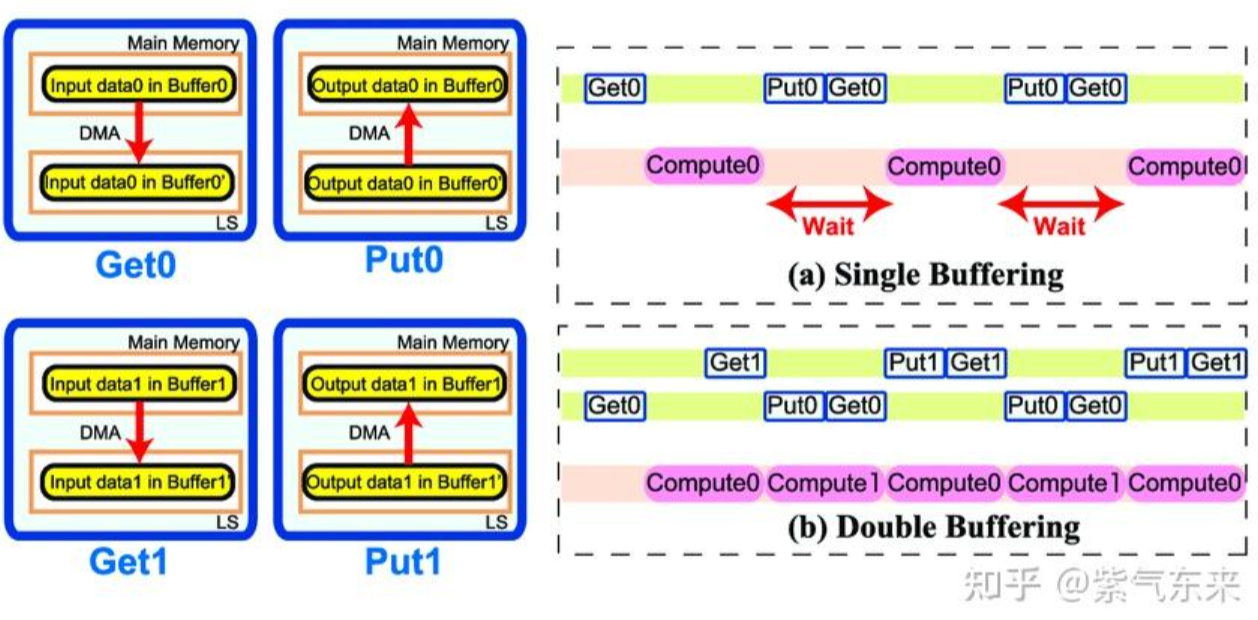
image-20250508191629076

  具体到代码实现中，主要有一下几个点：

  • 需要原来两倍的Shared Memory
  • 第一次加载数据在主循环之前，最后一次计算在主循环之后，主循环从 k = 1开始
  • 由于计算和下一次访存使用的Shared Memory不同，因此主循环中每次循环只需要一次__syncthreads()
  • GPU不能像CPU那样支持乱序执行，主循环中需要先将下一次循环计算需要的数据从Gloabal Memory中load 到寄存器，然后进行本次计算，之后再将load到寄存器中的数据写到Shared Memory，这样在LDG指令向Global Memory做load时，不会影响后续FFMA及其它运算指令的 launch 执行，也就达到了Double Buffering的目的。

  关于第四个点，还是挺深奥的，涉及GPU指令的流水线化和异步内存访问。一开始，我在想，既然GPU不能乱序执行，那么不还是串行吗？实则不然。答案如下，懒得自己总结了。

image-20250508194642841

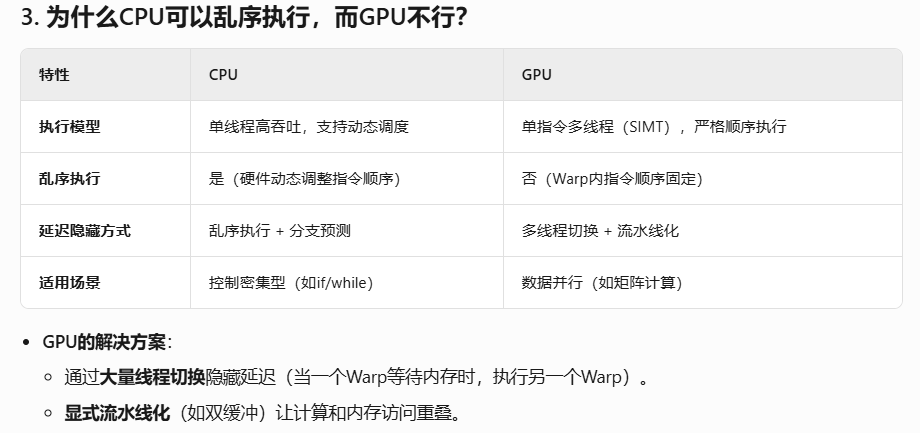
image-20250508194700041

还有一个问题就是LDG是异步的话，那么会不会存在数据竞争导致错误呢？

  答案是不会。硬件会自动插入依赖屏障，保证正确性。类似于CPU的load指令可以乱序执行，但编译器/硬件会保证数据依赖的正确性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
// 流水并行化：Double Buffering
__global__ void sgemm_V3(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c, const int M, const int N, const int K)
{
    const int bx = blockIdx.x;
    const int by = blockIdx.y;
    const int tx = threadIdx.x;
    const int ty = threadIdx.y;
    const int tid = ty * blockDim.x + tx;

    __shared__ float s_a[2][BK][BM];
    __shared__ float s_b[2][BK][BN];

    float r_c[TM][TN] = {0.0};
    float r_load_a[4];
    float r_load_b[4];
    float r_comp_a[TM];
    float r_comp_b[TN];

    int load_a_smem_m = tid >> 1;
    int load_a_smem_k = (tid & 1) << 2;
    int load_b_smem_k = tid >> 5;
    int load_b_smem_n = (tid & 31) << 2;

    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    {
        int load_a_gmem_k = load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        int load_b_gmem_k = load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);

        s_a[0][load_a_smem_k][load_a_smem_m] = r_load_a[0];
        s_a[0][load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
        s_a[0][load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
        s_a[0][load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
        FLOAT4(s_b[0][load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);
    }


    int cnt = (K + BK - 1) / BK;
    for(int bk = 1; bk < cnt; ++bk)
    {
        int smem_sel = (bk - 1) & 1;
        int smem_sel_next = bk & 1;

        int load_a_gmem_k = bk * BK + load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        int load_b_gmem_k = bk * BK + load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);

        #pragma unroll
        for(int k = 0; k < BK; ++k)
        {
            FLOAT4(r_comp_a[0]) = FLOAT4(s_a[smem_sel][k][ty * TM / 2]);
            FLOAT4(r_comp_a[4]) = FLOAT4(s_a[smem_sel][k][ty * TM / 2 + BM / 2]);
            FLOAT4(r_comp_b[0]) = FLOAT4(s_b[smem_sel][k][tx * TN / 2]);
            FLOAT4(r_comp_b[4]) = FLOAT4(s_b[smem_sel][k][tx * TN / 2 + BN / 2]);

            #pragma unroll
            for(int m = 0; m < TM; ++m)
            {
                #pragma unroll
                for(int n = 0; n < TN; ++n) r_c[m][n] += r_comp_a[m] * r_comp_b[n];
            }
        }

        s_a[smem_sel_next][load_a_smem_k][load_a_smem_m] = r_load_a[0];
        s_a[smem_sel_next][load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
        s_a[smem_sel_next][load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
        s_a[smem_sel_next][load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
        FLOAT4(s_b[smem_sel_next][load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);

        __syncthreads();
    }

    #pragma unroll
    for(int k = 0; k < BK; ++k)
    {
        FLOAT4(r_comp_a[0]) = FLOAT4(s_a[1][k][ty * TM / 2]);
        FLOAT4(r_comp_a[4]) = FLOAT4(s_a[1][k][ty * TM / 2 + BM / 2]);
        FLOAT4(r_comp_b[0]) = FLOAT4(s_b[1][k][tx * TN / 2]);
        FLOAT4(r_comp_b[4]) = FLOAT4(s_b[1][k][tx * TN / 2 + BN / 2]);

        #pragma unroll
        for(int m = 0; m < TM; ++m)
        {
            #pragma unroll
            for(int n = 0; n < TN; ++n) r_c[m][n] += r_comp_a[m] * r_comp_b[n];
        }
    }

    #pragma unroll
    for(int i = 0; i < TM / 2; ++i)
    {
        int store_c_gmem_m = by * BM + ty * TM / 2 + i;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i][4]);
    }

    #pragma unroll
    for(int i = 0; i < TM / 2; ++i)
    {
        int store_c_gmem_m = by * BM + ty * TM / 2 + i + BM / 2;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i + TM / 2][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i + TM / 2][4]);
    }

}

  计算结果如下,性能达到了理论峰值的75.7%，达到了实际可达峰值的90%：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
M N K =    128    128   1024, Time =   0.00011162   0.00011725   0.00012186 s, AVG Performance =   286.1834 Gflops
M N K =    192    192   1024, Time =   0.00011059   0.00011192   0.00011264 s, AVG Performance =   674.5471 Gflops
M N K =    256    256   1024, Time =   0.00011155   0.00011243   0.00011469 s, AVG Performance =  1193.8020 Gflops
M N K =    384    384   1024, Time =   0.00010957   0.00011162   0.00011366 s, AVG Performance =  2705.6147 Gflops
M N K =    512    512   1024, Time =   0.00010854   0.00010957   0.00011469 s, AVG Performance =  4899.8878 Gflops
M N K =    768    768   1024, Time =   0.00010957   0.00011038   0.00011162 s, AVG Performance = 10943.2485 Gflops
M N K =   1024   1024   1024, Time =   0.00010957   0.00011132   0.00011776 s, AVG Performance = 19291.3629 Gflops
M N K =   1536   1536   1024, Time =   0.00021299   0.00021944   0.00022221 s, AVG Performance = 22019.2705 Gflops
M N K =   2048   2048   1024, Time =   0.00043715   0.00044431   0.00045056 s, AVG Performance = 19333.1840 Gflops
M N K =   3072   3072   1024, Time =   0.00090624   0.00091166   0.00091648 s, AVG Performance = 21200.2324 Gflops
M N K =   4096   4096   1024, Time =   0.00149094   0.00151910   0.00167629 s, AVG Performance = 22618.4236 Gflops
M N K =   6144   6144   1024, Time =   0.00334234   0.00342294   0.00378880 s, AVG Performance = 22585.6909 Gflops
M N K =   8192   8192   1024, Time =   0.00587981   0.00618916   0.00649728 s, AVG Performance = 22206.4044 Gflops
M N K =  12288  12288   1024, Time =   0.01135514   0.01144668   0.01189990 s, AVG Performance = 27015.4839 Gflops
M N K =  16384  16384   1024, Time =   0.02017075   0.02207642   0.02387558 s, AVG Performance = 24902.4032 Gflops

2.5 cuBLAS 性能

  性能达到了理论峰值的83.9%，实际可达峰值的99%：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
M N K =    128    128   1024, Time =   0.00001843   0.00035505   0.00335494 s, AVG Performance =    94.5063 Gflops
M N K =    192    192   1024, Time =   0.00002253   0.00026675   0.00245965 s, AVG Performance =   283.0250 Gflops
M N K =    256    256   1024, Time =   0.00002662   0.00003389   0.00008397 s, AVG Performance =  3959.8791 Gflops
M N K =    384    384   1024, Time =   0.00003174   0.00003840   0.00005530 s, AVG Performance =  7864.9753 Gflops
M N K =    512    512   1024, Time =   0.00005120   0.00005386   0.00006554 s, AVG Performance =  9967.4525 Gflops
M N K =    768    768   1024, Time =   0.00008602   0.00009175   0.00013824 s, AVG Performance = 13165.7144 Gflops
M N K =   1024   1024   1024, Time =   0.00012698   0.00013035   0.00014438 s, AVG Performance = 16474.4968 Gflops
M N K =   1536   1536   1024, Time =   0.00022211   0.00023521   0.00034304 s, AVG Performance = 20542.9712 Gflops
M N K =   2048   2048   1024, Time =   0.00042496   0.00042792   0.00044544 s, AVG Performance = 20073.5427 Gflops
M N K =   3072   3072   1024, Time =   0.00084992   0.00085535   0.00088269 s, AVG Performance = 22595.9154 Gflops
M N K =   4096   4096   1024, Time =   0.00146125   0.00146872   0.00149606 s, AVG Performance = 23394.2915 Gflops
M N K =   6144   6144   1024, Time =   0.00306682   0.00307189   0.00308838 s, AVG Performance = 25166.7152 Gflops
M N K =   8192   8192   1024, Time =   0.00457830   0.00470508   0.00521523 s, AVG Performance = 29210.7880 Gflops
M N K =  12288  12288   1024, Time =   0.01022771   0.01032509   0.01057178 s, AVG Performance = 29950.1034 Gflops
M N K =  16384  16384   1024, Time =   0.01822106   0.01895342   0.01967821 s, AVG Performance = 29005.6252 Gflops

3. Hgemm

  半精度浮点类型的矩阵乘法，使用tensor core。

3.1 前置知识

3.1.1 cublas的调用

cublas有个诡异的列优先原则，导致这个函数接口的传参不是那么容易，要好好注意这个是否转置、两个矩阵的顺序、主维等参数。给出两种方法：

1
2
3
4
5
6
7
8
9
10
11
12
//第一种：诡异先b再a
HGEMM_CHECK_CUBLAS_ERROR(cublasGemmEx(handle,
                                      CUBLAS_OP_N,
                                      CUBLAS_OP_N,
                                      N, M, K,
                                      &alpha,
                                      B, CUDA_R_16F, N,
                                      A, CUDA_R_16F, K,
                                      &beta,
                                      C, CUDA_R_16F, N,
                                      CUBLAS_COMPUTE_16F,
                                      CUBLAS_GEMM_DEFAULT_TENSOR_OP));

第二种：喜欢转置说是image-20250701011406779

两种都能求的正确结果，但是明显方法1更好，因为不用转置，毕竟矩阵大了的话，转置需要的时间也不小。参考blog：有关CUBLAS中的矩阵乘法函数 - 爨爨爨好 - 博客园

3.1.2 tensor core api

  这里我们以D = A * B + C 为例。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 着重注意第一个参数和最后一个参数
// 作为A和B分别是wmma::matrix_a和wmma::matrix_b
// 用作源或目标累加器（C 或 D）时使用accumulator
// 对于 matrix_a 和 matrix_b 片段，必须指定 Layout 参数, 累加器不用填
nvcuda::wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> frag_a;
nvcuda::wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> frag_a;
nvcuda::wmma::fragment<wmma::accumulator, 16, 16, 16, half> frag_c;

nvcuda::wmma::fill_fragment(frag_c, 0.0);
nvcuda::wmma::load_matrix_sync(frag_a, (shared memory or global memory pointer), (stride_a));
nvcuda::wmma::load_matrix_sync(frag_b, (shared memory or global memory pointer), (stride_b));
nvcuda::wmma::mma_sync(frag_c, frag_a, frag_b, frag_c);
nvcuda::wmma::store_matrix_sync((shared memory or global memory pointer), frag_c, (stride_c), wmma::mem_row_major);

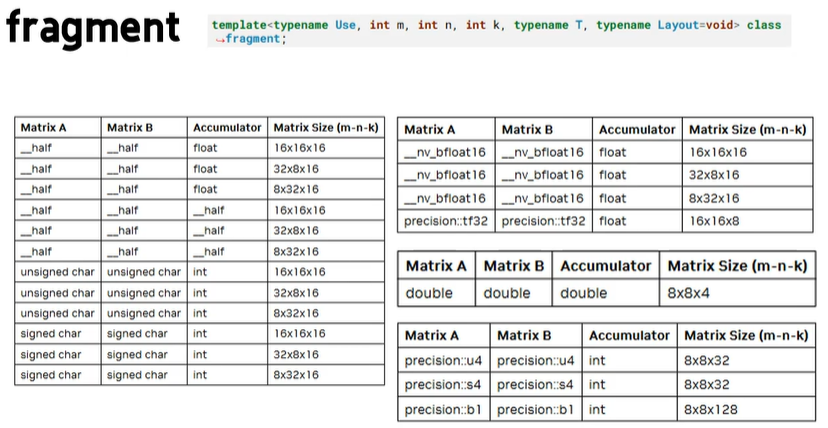
image-20250701193517088

3.1.3 ptx 指令

  • ldmatrix

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    #define LDMATRIX_X1(R, addr) \
        asm volatile("ldmatrix.sync.aligned.x1.m8n8.shared.b16 {%0}, [%1];\n" : "=r"(R) : "r"(addr))

    #define LDMATRIX_X2(R0, R1, addr) \
        asm volatile("ldmatrix.sync.aligned.x2.m8n8.shared.b16 {%0, %1}, [%2];\n" : "=r"(R0), "=r"(R1) : "r"(addr))

    #define LDMATRIX_X4(R0, R1, R2, R3, addr)                                             \
        asm volatile("ldmatrix.sync.aligned.x4.m8n8.shared.b16 {%0, %1, %2, %3}, [%4];\n" \
                     : "=r"(R0), "=r"(R1), "=r"(R2), "=r"(R3)                             \
                     : "r"(addr))

    LDMATRIX_X1:加载一块8x8的半精度（b16）矩阵tile（通常为Tensor Core的数据载入方式）从shared memory 到单个寄存器（R）。

    • ldmatrix：矩阵块加载PTX指令
    • .sync.aligned：同步、对齐方式
    • .x1：一次加载1个tile（8x8）
    • .m8n8：tile大小8x8

    • .shared.b16：从shared memory以16位为单位加载(每 16 位为一个数据元素)

    • .x2：每次加载2个tile

    • .x4：每次加载4个tile

  • HMMA16816

    1
    2
    3
    4
    #define HMMA16816(RD0, RD1, RA0, RA1, RA2, RA3, RB0, RB1, RC0, RC1)                                                    \
        asm volatile("mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16 {%0, %1}, {%2, %3, %4, %5}, {%6, %7}, {%8, %9};\n" \
                     : "=r"(RD0), "=r"(RD1)                                                                                \
                     : "r"(RA0), "r"(RA1), "r"(RA2), "r"(RA3), "r"(RB0), "r"(RB1), "r"(RC0), "r"(RC1))
    • mma：矩阵-矩阵累加（Matrix Multiply Accumulate）PTX指令
    • .sync.aligned：同步、对齐
    • .m16n8k16：矩阵维度（MxN乘K）
    • .row.col：内存布局（行主序/列主序）
    • f16.f16.f16.f16：操作数和结果全为半精度float16
    • 输出：
      • {%0, %1}：结果D的两个寄存器
    • 输入：
      • RA0~RA3、RB0~RB1：A和B矩阵块的寄存器
      • RC0, RC1：累加用的C寄存器

  • CP_ASYNC

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    #if ((__CUDACC_VER_MAJOR__ == 11) && (__CUDACC_VER_MINOR__ >= 4)) || (__CUDACC_VER_MAJOR__ > 11)
    #define CP_ASYNC_CA(dst, src, Bytes) \
        asm volatile("cp.async.ca.shared.global.L2::128B [%0], [%1], %2;\n" ::"r"(dst), "l"(src), "n"(Bytes))

    #define CP_ASYNC_CG(dst, src, Bytes) \
        asm volatile("cp.async.cg.shared.global.L2::128B [%0], [%1], %2;\n" ::"r"(dst), "l"(src), "n"(Bytes))
    #else
    #define CP_ASYNC_CA(dst, src, Bytes) \
        asm volatile("cp.async.ca.shared.global [%0], [%1], %2;\n" ::"r"(dst), "l"(src), "n"(Bytes))

    #define CP_ASYNC_CG(dst, src, Bytes) \
        asm volatile("cp.async.cg.shared.global [%0], [%1], %2;\n" ::"r"(dst), "l"(src), "n"(Bytes))
    #endif

    #define CP_ASYNC_COMMIT_GROUP() asm volatile("cp.async.commit_group;\n" ::)

    #define CP_ASYNC_WAIT_GROUP(N) asm volatile("cp.async.wait_group %0;\n" ::"n"(N))

    #define CP_ASYNC_WAIT_ALL() asm volatile("cp.async.wait_all;\n" ::)

    CUDA 11.4 及以上:

    • cp.async：CUDA 8.0+ 新增的异步数据拷贝PTX指令（copy async），用于把全局内存数据异步搬到 shared memory。
    • ca：cache all（全层缓存提示），告诉硬件这次搬运要经过所有缓存。
    • cg：cache global（只缓存到 L1，跳过 L2）。
    • .L2::128B：新语法，指明此次操作对 L2 cache 的控制方式（128 字节对齐/搬运），增加细粒度 cache 控制（11.4 新特性）。
    • shared.global：从全局内存搬到共享内存。
    • [%0]：目标 shared memory 地址（dst）。
    • [%1]：源全局内存地址（src）。
    • %2：要搬运的字节数（Bytes）。

    CUDA 11.3 及一下：只是没有 .L2::128B 后缀。因为11.4之前 PTX不支持L2 cache细粒度控

    • cp.async.commit_group：告诉GPU，在这之前的cp.async属于一组，并不是到这条命令的时候才会开始运行，之前就开始了。
    • cp.async.wait_group %0：等待一个 已提交的异步拷贝操作组 完成。类似于 CUDA 的 __syncthreads()，但仅针对异步拷贝操作，而不是全部线程同步。

  关于这些api 和 指令，不如直接看下面有例子，看例子更好理解。

3.2 v1

  首先讨论BM等数据的选取，具体数值来源于其他博客的分析。

  BM和BN是越大越好，然后打算选取16*16*16的的tensor core，BK至少需要是nvcuda::wmma::fragment中定义矩阵的K维度的整数倍；当BK太小（例如取BK = 16）时，核心循环中HMMA指令占比不高，一些循环相关的地址计算的指令会导致性能下降；当BK >= 32时，发现性能基本不会再随BK而提高了；加之hared memory、Registers的限制，最终取BM = 128，BN = 256，BK = 32，thread_per_block = 256。

  这样每次K循环中，256个线程每个线程需要取16个矩阵A的元素，取32个矩阵B的元素；8个warp每个warp负责计算64x32x64的矩阵乘法。为了方便起见假设M/N/K对齐到128/256/32，也就是没有处理corner case。

  调用的C++ wmma的API，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
__global__ void myHGEMMAlignedV1(half * __restrict__ a, half * __restrict__ b, half * __restrict__ c,
                                const int M, const int N, const int K)
{
    const int BM = 128;
    const int BN = 256;
    const int BK = 32;

    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tid = threadIdx.x;
    int wid = tid >> 5;

    const int APAD = 8;
    const int BPAD = 8;

    __shared__ half s_a[BM][BK + APAD];
    __shared__ half s_b[BK][BN + BPAD];

    wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> frag_a[2][4];
    wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> frag_b[2][4];
    wmma::fragment<wmma::accumulator, 16, 16, 16, half> frag_c[4][4];

    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::fill_fragment(frag_c[i][j], 0.0);
        }
    }

    int load_a_smem_m = (tid >> 2) << 1;
    int load_a_smem_k = (tid & 3) << 3;
    int load_b_smem_k = (tid >> 5) << 2;
    int load_b_smem_n = (tid & 31) << 3;

    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_smem_k, K);
    int load_b_gmem_addr = OFFSET(load_b_smem_k, load_b_gmem_n, N);

    int comp_c_frag_m = wid & 1;
    int comp_c_frag_n = wid >> 1;

    for(int bk = 0; bk < K / BK; ++bk)
    {
        FLOAT4(s_a[load_a_smem_m][load_a_smem_k]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(s_a[load_a_smem_m + 1][load_a_smem_k]) = FLOAT4(a[load_a_gmem_addr + K]);

        FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr]);
        FLOAT4(s_b[load_b_smem_k + 1][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr + N]);
        FLOAT4(s_b[load_b_smem_k + 2][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr + 2 * N]);
        FLOAT4(s_b[load_b_smem_k + 3][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr + 3 * N]);
        
        load_a_gmem_addr += BK;
        load_b_gmem_addr += BK * N;

        __syncthreads();

        // 取的一个16*16的块，整个warp协作取
        wmma::load_matrix_sync(frag_a[0][0], &s_a[comp_c_frag_m * 64][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][1], &s_a[comp_c_frag_m * 64 + 16][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][2], &s_a[comp_c_frag_m * 64 + 32][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][3], &s_a[comp_c_frag_m * 64 + 48][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][0], &s_a[comp_c_frag_m * 64][16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][1], &s_a[comp_c_frag_m * 64 + 16][16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][2], &s_a[comp_c_frag_m * 64 + 32][16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][3], &s_a[comp_c_frag_m * 64 + 48][16], BK + APAD);

        wmma::load_matrix_sync(frag_b[0][0], &s_b[0][comp_c_frag_n * 64], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][1], &s_b[0][comp_c_frag_n * 64 + 16], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][2], &s_b[0][comp_c_frag_n * 64 + 32], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][3], &s_b[0][comp_c_frag_n * 64 + 48], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][0], &s_b[16][comp_c_frag_n * 64], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][1], &s_b[16][comp_c_frag_n * 64 + 16], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][2], &s_b[16][comp_c_frag_n * 64 + 32], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][3], &s_b[16][comp_c_frag_n * 64 + 48], BN + BPAD);
    
        #pragma unroll
        for(int i = 0; i < 4; ++i)
        {
            #pragma unroll
            for(int j = 0; j < 4; ++j)
            {
                wmma::mma_sync(frag_c[i][j], frag_a[0][i], frag_b[0][j], frag_c[i][j]);
                wmma::mma_sync(frag_c[i][j], frag_a[1][i], frag_b[1][j], frag_c[i][j]);
            }
        }

        __syncthreads();
    }

    int store_c_gmem_m = by * BM + comp_c_frag_m * 64;
    int store_c_gmem_n = bx * BN + comp_c_frag_n * 64;
    int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);

    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::store_matrix_sync(&c[store_c_gmem_addr + i * 16 * N + j * 16], frag_c[i][j], N, wmma::mem_row_major);
        }
    }

}

  这里有三个疑问，一是每个线程取16个矩阵A的元素，目前是每个线程取相邻两行的连续8列，而不是取一行的16列。关于为什么要这样？

  没找到准确的回答，大体上是有利于合并访存、方便后续共享内存布局、WMMA tile加载、更好地支持多warp并行，避免共享内存bank conflict。

  二是关于frag_a的填充，发现frag_a的列坐标在增加，而对应读取的s_a是行坐标在+16，这样写是否是出于优化的角度？是否将frag_a的定义改成frag[4][2]更符合语义？

  并不是出于优化的角度，只是通常的代码习惯。主流的wmma相关代码习惯是BK方向在前（方便做K方向累加），M/N方向在后，并且方便后面wmma::mma_sync的调用。

  三是关于bank confilct的解决，这里是通过加了16 Bytes的pad解决的，为什么能解决？

  关于这个，我并没有想明白，这部分对smem的读取是warp协作读取的，我不会确定每个线程读取哪些数据，但是它应该是确实能避免的，并且这似乎也是一种官方常用方式。

3.3 Hgemm v2: Global Memory到Shared Memory的异步拷贝

  对全局内存的访问通过异步拷贝实现，即利用前面提到的cp.async指令，注意smem的首地址要用__cvta_generic_to_shared()获取，具体看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
__global__ void myHGEMMAlignedV2(half * __restrict__ a, half * __restrict__ b, half * __restrict__ c,
                                const int M, const int N, const int K){
    
    const int BM = 128;
    const int BN = 256;
    const int BK = 32;

    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tid = threadIdx.x;
    int wid = tid >> 5;

    const int APAD = 8;
    const int BPAD = 8;

    __shared__ half s_a[BM][BK + APAD];
    __shared__ half s_b[BK][BN + BPAD];

    wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> frag_a[2][4];
    wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> frag_b[2][4];
    wmma::fragment<wmma::accumulator, 16, 16, 16, half> frag_c[4][4];

    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::fill_fragment(frag_c[i][j], 0.0);
        }
    }

    int load_a_smem_m = (tid >> 2) << 1;
    int load_a_smem_k = (tid & 3) << 3;
    int load_b_smem_k = (tid >> 5) << 2;
    int load_b_smem_n = (tid & 31) << 3;

    int s_a_base_addr = __cvta_generic_to_shared(s_a[0]);
    int s_b_base_addr = __cvta_generic_to_shared(s_b[0]);
    
    int load_a_smem_addr_0 = s_a_base_addr + OFFSET(load_a_smem_m, load_a_smem_k, BK + APAD) * sizeof(half);
    int load_a_smem_addr_1 = load_a_smem_addr_0 + (BK + APAD) * sizeof(half);
    
    int load_b_smem_addr_0 = s_b_base_addr + OFFSET(load_b_smem_k, load_b_smem_n, BN + BPAD) * sizeof(half);
    int load_b_smem_addr_1 = load_b_smem_addr_0 + (BN + BPAD) * sizeof(half);
    int load_b_smem_addr_2 = load_b_smem_addr_0 + 2 * (BN + BPAD) * sizeof(half);
    int load_b_smem_addr_3 = load_b_smem_addr_0 + 3 * (BN + BPAD) * sizeof(half);
    
    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_smem_k, K);
    int load_b_gmem_addr = OFFSET(load_b_smem_k, load_b_gmem_n, N);

    int comp_c_frag_m = wid & 1;
    int comp_c_frag_n = wid >> 1;

    for(int bk = 0; bk < K / BK; ++bk)
    {
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
            : "r"(load_a_smem_addr_0), "l"(&a[load_a_gmem_addr]));
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
            : "r"(load_a_smem_addr_1), "l"(&a[load_a_gmem_addr + K]));
        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
            : "r"(load_b_smem_addr_0), "l"(&b[load_b_gmem_addr]));        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
            : "r"(load_b_smem_addr_1), "l"(&b[load_b_gmem_addr + N]));
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
            : "r"(load_b_smem_addr_2), "l"(&b[load_b_gmem_addr + 2 * N]));        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
            : "r"(load_b_smem_addr_3), "l"(&b[load_b_gmem_addr + 3 * N]));
            
        asm ("cp.async.commit_group;\n" ::);
        asm ("cp.async.wait_group 0;\n" ::);

        load_a_gmem_addr += BK;
        load_b_gmem_addr += BK * N;

        __syncthreads();

        wmma::load_matrix_sync(frag_a[0][0], &s_a[comp_c_frag_m * 64][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][1], &s_a[comp_c_frag_m * 64 + 16][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][2], &s_a[comp_c_frag_m * 64 + 32][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][3], &s_a[comp_c_frag_m * 64 + 48][0], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][0], &s_a[comp_c_frag_m * 64][16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][1], &s_a[comp_c_frag_m * 64 + 16][16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][2], &s_a[comp_c_frag_m * 64 + 32][16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][3], &s_a[comp_c_frag_m * 64 + 48][16], BK + APAD);

        wmma::load_matrix_sync(frag_b[0][0], &s_b[0][comp_c_frag_n * 64], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][1], &s_b[0][comp_c_frag_n * 64 + 16], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][2], &s_b[0][comp_c_frag_n * 64 + 32], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][3], &s_b[0][comp_c_frag_n * 64 + 48], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][0], &s_b[16][comp_c_frag_n * 64], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][1], &s_b[16][comp_c_frag_n * 64 + 16], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][2], &s_b[16][comp_c_frag_n * 64 + 32], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][3], &s_b[16][comp_c_frag_n * 64 + 48], BN + BPAD);

        #pragma unroll
        for(int i = 0; i < 4; ++i)
        {
            #pragma unroll
            for(int j = 0; j < 4; ++j)
            {
                wmma::mma_sync(frag_c[i][j], frag_a[0][i], frag_b[0][j], frag_c[i][j]);
                wmma::mma_sync(frag_c[i][j], frag_a[1][i], frag_b[1][j], frag_c[i][j]);
            }
        }

        __syncthreads();
    }

    int store_c_gmem_m = by * BM + comp_c_frag_m * 64;
    int store_c_gmem_n = bx * BN + comp_c_frag_n * 64;
    int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);

    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::store_matrix_sync(&c[store_c_gmem_addr + i * 16 * N + j * 16], frag_c[i][j], N, wmma::mem_row_major);
        }
    }

}

  

3.4 v2: Double Buffer

  Sgemm中详细介绍过，不多废话了，需要注意的是double buffer会用到两倍的shared memory，当使用的shared memory超过48 KB时，需要使用dynamic shared memory。kernel的怕配置和调用方式如下：

1
2
3
4
5
6
7
8
9
10
const int BM = 128, BN = 256, BK = 32;
dim3 blockDim(256);
int BX = (N + BN - 1) / BN;
int BY = (M + BM - 1) / BM;
dim3 gridDim(BX, BY);

cudaFuncSetAttribute(myHGEMMAlignedV3, cudaFuncAttributeMaxDynamicSharedMemorySize, 98304);

unsigned int dsmem = 2 * (BM * (BK + 8) + BK * (BN + 8)) * sizeof(half);
myHGEMMAlignedV3<<<gridDim, blockDim, dsmem>>>(a, b, c, M, N, K);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
__global__ void myHGEMMAlignedV3(half * __restrict__ a, half * __restrict__ b, half * __restrict__ c,
    const int M, const int N, const int K){

    const int BM = 128;
    const int BN = 256;
    const int BK = 32;

    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tid = threadIdx.x;
    int wid = tid >> 5;

    const int APAD = 8;
    const int BPAD = 8;

    extern __shared__ half smem[];
    half *s_a = smem;
    half *s_b = smem + 2 * BM * (BK + APAD);
    int s_a_db_offset = BM * (BK + APAD);
    int s_b_db_offset = BK * (BN + BPAD);

    wmma::fragment<wmma::matrix_a, 16, 16, 16, half, wmma::row_major> frag_a[2][4];
    wmma::fragment<wmma::matrix_b, 16, 16, 16, half, wmma::row_major> frag_b[2][4];
    wmma::fragment<wmma::accumulator, 16, 16, 16, half> frag_c[4][4];

    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::fill_fragment(frag_c[i][j], 0.0);
        }
    }

    int load_a_smem_m = (tid >> 2) << 1;
    int load_a_smem_k = (tid & 3) << 3;
    int load_b_smem_k = (tid >> 5) << 2;
    int load_b_smem_n = (tid & 31) << 3;

    int s_a_base_addr = __cvta_generic_to_shared(s_a);
    int s_b_base_addr = __cvta_generic_to_shared(s_b);

    int load_a_smem_addr_0 = s_a_base_addr + OFFSET(load_a_smem_m, load_a_smem_k, BK + APAD) * sizeof(half);
    int load_a_smem_addr_1 = load_a_smem_addr_0 + (BK + APAD) * sizeof(half);

    int load_b_smem_addr_0 = s_b_base_addr + OFFSET(load_b_smem_k, load_b_smem_n, BN + APAD) * sizeof(half);
    int load_b_smem_addr_1 = load_b_smem_addr_0 + (BN + APAD) * sizeof(half);
    int load_b_smem_addr_2 = load_b_smem_addr_0 + 2 * (BN + APAD) * sizeof(half);
    int load_b_smem_addr_3 = load_b_smem_addr_0 + 3 * (BN + APAD) * sizeof(half);

    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_smem_k, K);
    int load_b_gmem_addr = OFFSET(load_b_smem_k, load_b_gmem_n, N);

    int comp_c_frag_m = wid & 1;
    int comp_c_frag_n = wid >> 1;
    
    {
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_a_smem_addr_0), "l"(&a[load_a_gmem_addr]));
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_a_smem_addr_1), "l"(&a[load_a_gmem_addr + K]));

        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_0), "l"(&b[load_b_gmem_addr]));        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_1), "l"(&b[load_b_gmem_addr + N]));
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_2), "l"(&b[load_b_gmem_addr + 2 * N]));        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_3), "l"(&b[load_b_gmem_addr + 3 * N]));

        asm ("cp.async.commit_group;\n" ::);
        asm ("cp.async.wait_group 0;\n" ::);

        __syncthreads();
    }

    int smem_sel, smem_sel_next;

    for(int bk = 1; bk < K / BK; ++bk)
    {
        smem_sel = (bk & 1) ^ 1;
        smem_sel_next = ((bk - 1) & 1) ^ 1;

        load_a_gmem_addr += BK;
        load_b_gmem_addr += BK * N;
        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_a_smem_addr_0 + smem_sel_next * s_a_db_offset * (int)sizeof(half)), "l"(&a[load_a_gmem_addr]));
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_a_smem_addr_1 + smem_sel_next * s_a_db_offset * (int)sizeof(half)), "l"(&a[load_a_gmem_addr + K]));

        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_0 + smem_sel_next * s_b_db_offset * (int)sizeof(half)), "l"(&b[load_b_gmem_addr]));        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_1 + smem_sel_next * s_b_db_offset * (int)sizeof(half)), "l"(&b[load_b_gmem_addr + N]));
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_2 + smem_sel_next * s_b_db_offset * (int)sizeof(half)), "l"(&b[load_b_gmem_addr + 2 * N]));        
        asm ("cp.async.ca.shared.global [%0], [%1], 16;\n" :
        : "r"(load_b_smem_addr_3 + smem_sel_next * s_b_db_offset * (int)sizeof(half)), "l"(&b[load_b_gmem_addr + 3 * N]));

        wmma::load_matrix_sync(frag_a[0][0], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64) * (BK + APAD)], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][1], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 16) * (BK + APAD)], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][2], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 32) * (BK + APAD)], BK + APAD);
        wmma::load_matrix_sync(frag_a[0][3], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 48) * (BK + APAD)], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][0], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64) * (BK + APAD) + 16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][1], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 16) * (BK + APAD) + 16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][2], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 32) * (BK + APAD) + 16], BK + APAD);
        wmma::load_matrix_sync(frag_a[1][3], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 48) * (BK + APAD) + 16], BK + APAD);

        wmma::load_matrix_sync(frag_b[0][0], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][1], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64 + 16], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][2], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64 + 32], BN + BPAD);
        wmma::load_matrix_sync(frag_b[0][3], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64 + 48], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][0], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][1], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64 + 16], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][2], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64 + 32], BN + BPAD);
        wmma::load_matrix_sync(frag_b[1][3], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64 + 48], BN + BPAD);

        #pragma unroll
        for(int i = 0; i < 4; ++i)
        {
            #pragma unroll
            for(int j = 0; j < 4; ++j)
            {
                wmma::mma_sync(frag_c[i][j], frag_a[0][i], frag_b[0][j], frag_c[i][j]);
                wmma::mma_sync(frag_c[i][j], frag_a[1][i], frag_b[1][j], frag_c[i][j]);
            }
        }

        asm ("cp.async.commit_group;\n" ::);
        asm ("cp.async.wait_group 0;\n" ::);

        __syncthreads();
    }

    smem_sel = ((K / BK) & 1) ^ 1;
    
    wmma::load_matrix_sync(frag_a[0][0], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64) * (BK + APAD)], BK + APAD);
    wmma::load_matrix_sync(frag_a[0][1], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 16) * (BK + APAD)], BK + APAD);
    wmma::load_matrix_sync(frag_a[0][2], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 32) * (BK + APAD)], BK + APAD);
    wmma::load_matrix_sync(frag_a[0][3], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 48) * (BK + APAD)], BK + APAD);
    wmma::load_matrix_sync(frag_a[1][0], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64) * (BK + APAD) + 16], BK + APAD);
    wmma::load_matrix_sync(frag_a[1][1], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 16) * (BK + APAD) + 16], BK + APAD);
    wmma::load_matrix_sync(frag_a[1][2], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 32) * (BK + APAD) + 16], BK + APAD);
    wmma::load_matrix_sync(frag_a[1][3], &s_a[smem_sel * s_a_db_offset + (comp_c_frag_m * 64 + 48) * (BK + APAD) + 16], BK + APAD);

    wmma::load_matrix_sync(frag_b[0][0], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64], BN + BPAD);
    wmma::load_matrix_sync(frag_b[0][1], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64 + 16], BN + BPAD);
    wmma::load_matrix_sync(frag_b[0][2], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64 + 32], BN + BPAD);
    wmma::load_matrix_sync(frag_b[0][3], &s_b[smem_sel * s_b_db_offset + comp_c_frag_n * 64 + 48], BN + BPAD);
    wmma::load_matrix_sync(frag_b[1][0], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64], BN + BPAD);
    wmma::load_matrix_sync(frag_b[1][1], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64 + 16], BN + BPAD);
    wmma::load_matrix_sync(frag_b[1][2], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64 + 32], BN + BPAD);
    wmma::load_matrix_sync(frag_b[1][3], &s_b[smem_sel * s_b_db_offset + 16 * (BN + BPAD) + comp_c_frag_n * 64 + 48], BN + BPAD);
    
    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::mma_sync(frag_c[i][j], frag_a[0][i], frag_b[0][j], frag_c[i][j]);
            wmma::mma_sync(frag_c[i][j], frag_a[1][i], frag_b[1][j], frag_c[i][j]);
        }
    }

    int store_c_gmem_m = by * BM + comp_c_frag_m * 64;
    int store_c_gmem_n = bx * BN + comp_c_frag_n * 64;
    int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);

    #pragma unroll
    for(int i = 0; i < 4; ++i)
    {
        #pragma unroll
        for(int j = 0; j < 4; ++j)
        {
            wmma::store_matrix_sync(&c[store_c_gmem_addr + i * 16 * N + j * 16], frag_c[i][j], N, wmma::mem_row_major);
        }
    }

}

3.5 v4: 提高L2 Cache的局部性

  RTX3090一共有82个SM，经过计算v3的优化，每个SM只能容纳一个block，当大规模矩阵乘法的block数目超过82时，会按照gridDim.z -> gridDim.y -> gridDim.x这样的循环顺序进行调度。

  例如当M = N = K = 16384时，矩阵C会被分块成128 * 64个Tile，如果按照正常的调度顺序，先调度矩阵C第一行64个Tile对应的block加上第二行的前18个block，这样虽然矩阵A的局部性很好，但是矩阵B的访存局部性极差。所以考虑平衡矩阵A和矩阵B的局部性，现在改成第一次先调度第一行到第五行的前16个block，加上第六行的前2个block。

  主要需要做的是修改一下调用kernel时的代码，利用其默认的调度顺序，加上gridDim.z这一维，这里NSPLIT就代表矩阵C的一行一次调度NSPLIT列就改转到下一行（NSPLIT = 16 * 256 = 4096）：

1
2
3
4
5
6
7
8
9
10
11
12
13
const int BM = 128, BN = 256, BK = 32;
dim3 blockDim(256);
int BX = (N + BN - 1) / BN;
int BY = (M + BM - 1) / BM;

const int NSPLIT = 4096;
int split_num = (N + NSPLIT - 1) / NSPLIT;
dim3 gridDim((BX + split_num - 1) / split_num, BY, split_num);

cudaFuncSetAttribute(myHGEMMAlignedV4, cudaFuncAttributeMaxDynamicSharedMemorySize, 98304);

unsigned int dsmem = 2 * (BM * (BK + 8) + BK * (BN + 8)) * sizeof(half);
myHGEMMAlignedV4<<<gridDim, blockDim, dsmem>>>(a, b, c, M, N, K);
1
2
3
4
5
6
7
8
9
10
11
12
13
__global__ void myHGEMMAlignedV4(
    half * __restrict__ a, half * __restrict__ b, half * __restrict__ c,
    const int M, const int N, const int K) {

    // ...

    // int bx = blockIdx.x; // 原来是这样
    int bx = blockIdx.z * gridDim.x + blockIdx.x; // 现在是这样
    if (bx >= N / BN || by >= M / BM)
        return;

    // ...
}

3.6 v5: 循环展开

  主要修改是显式要求编译器对循环完全展开32次（如果 K/BK 比32大，则只会unroll前32次），没有显式的 #pragma unroll，即让编译器默认决定是否展开循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
__global__ void myHGEMMAlignedV5(
    half * __restrict__ a, half * __restrict__ b, half * __restrict__ c,
    const int M, const int N, const int K) {

    // ...

    #pragma unroll 32
    for (int bk = 1; bk < K / BK; bk++) {
        // ...
    }

    // ...
}

  关于hgemm这部分的性能，可以参考这篇文章的情况，实测和文中相差不大，v5最后最好的情况下达到了140TFLOPS。

4. 最后

  代码仓库：神秘链接

  3090上sgemm性能最好大约在27TFLOPS左右，cublas在30TFLOPS左右，达到了90%左右的性能，2080ti上cublas和sgemm的最好性能都在11TFLOPS，接近99%的性能。

  hgemm的话由于用了cp.async指令，只能在3090（sm_80）上跑，2080ti（sm_75）不支持，最好性能140TFLOPS左右，平均大概在130TFLOPS左右，cublas基本稳定在130TFLOPS之上，最好性能也在140TFLOPS左右。

Reference

  1. 从啥也不会到CUDA GEMM优化

  2. CUDA（三）：通用矩阵乘法：从入门到熟练

  3. https://github.com/ifromeast/cuda_learning/tree/main/03_gemm

  4. 深入浅出GPU优化系列：GEMM优化（二）

  5. [施工中] CUDA GEMM 理论性能分析与 kernel 优化

  6. CUDA SGEMM矩阵乘法优化笔记——从入门到cublas

  7. CUDA Ampere Tensor Core HGEMM 矩阵乘法优化笔记 —— Up To 131 TFLOPS!

  8. https://github.com/nicolaswilde/cuda-tensorcore-hgemm

  9. https://space.bilibili.com/218427631/video

  10. 有关CUBLAS中的矩阵乘法函数 - 爨爨爨好 - 博客园