PyG Use-Cases & Applications

发表于 分类于

PyG Use-Cases & Applications

1.通过邻居采样扩展GNN(Scaling GNNs via Neighbor Sampling)
2.点云处理 (Point Cloud Processing)
3.解释图神经网络(Explaining Graph Neural Networks)
4.浅节点嵌入(Shallow Node Embeddings)

1.通过邻居采样扩展GNN(Scaling GNNs via Neighbor Sampling)

  主要是针对节点级别的学习的过程。

  在大型图中的图神经网络（GNNs）中实现扩展是一个重要的挑战，特别是在工业和社交应用中。传统的深度神经网络通过将训练损失分解为单个样本（称为小批量Mini-batches)并近似精确梯度随机地进行训练，已知能够很好地扩展到大量数据中。然而，在图神经网络（GNNs）中，应用随机小批量训练是具有挑战性，这是因为图的节点和边之间的相互依赖性很强。具体来说，每个节点的表示（即嵌入）不仅依赖于它自己的特征，还依赖于它的邻居节点的嵌入，而这些邻居节点的嵌入又依赖于它们各自的邻居节点的嵌入。这种依赖关系是递归的，随着网络层数的增加，这种依赖性会迅速扩大。这种现象通常被称为邻居爆炸。

  GNNs通常以全批量方式执行是一种简单的解决方法，这种方法意味着在每次训练时，整个图的数据都会被加载到内存中，并且所有节点的嵌入都会在所有层中同时计算和更新。这种方法存在内存需求大、计算需要大、收敛速度慢、不可扩展等问题。因此，可扩展技术对于将 GNN 应用于大规模图是必不可少的，以缓解由Mini-batches训练引起的邻居爆炸问题。

  可扩展技术有节点采样、层采样或子图采样技术、将传播与预测分离。这部分主要讲解节点采样（Node-wise Sampling）。节点采样是一种解决邻居爆炸问题的有效方法。该方法通过限制每个节点只采样一部分邻居节点，从而减少计算量和内存使用。（节点采样和邻居采样是同一个意思）。

1.1邻居采样(Neighbor Sampling)

工作原理

  PyG通过torch_geometric.loader.NeighborLoader类实现邻居采样。邻居采样通过递归地为每个节点采样固定数量的邻居节点来工作，即对每个节点 $v$，最多采样 $k$ 个邻居节点。这种方法确保了整体的 $L$-跳邻域大小是有界的。

具体步骤

​ 1.初始化种子节点：从一组种子节点集合 $S$ 开始，初始化采样过程。

​ 2.递归采样邻居：对于每一跳，从当前节点集合 $S_i$ 中的每个节点，最多采样 $k$ 个邻居节点，形成下一跳的节点集合 $S_{i+1}$。

​ 3.重复步骤：继续对每一跳采样，直到达到预定的跳数 $L$。

​ 4.构建子图：最终结果是围绕每个种子节点 $S$ 的一个有向 $L$-跳子图，其中保证每个节点与至少一个种子节点之间有一条长度不超过 $L$ 的路径。

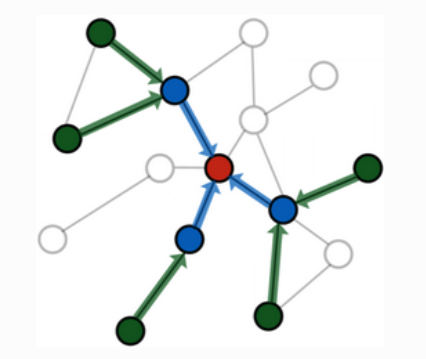
image-20240720004031177

存在的问题

  值得注意的是，邻域采样只能在一定程度上缓解邻域爆炸问题，因为整体邻域大小仍会随着层数的增加而呈指数增长。因此，通常不适合进行超过两到三跳的采样。

  通常情况下，采样的跳数和消息传递层数保持同步是合理的，因为采样更多跳数的数据无法被GNN的消息传递层利用。例如，如果GNN只有两层，那么采样三跳或更多邻居是浪费的，因为第三跳及其之后的节点特征不会被用到。尽管如此，如果需要使用更深层的GNN（超过两到三层），需要将采样的子图转换为双向子图，以确保正确的消息传递流。这样做可以使消息在反向路径上传递，确保节点之间的信息能够被有效整合。

  除了邻居采样，PyG还提供了其他适合更深层GNN的采样方法，例如：

  1. ClusterLoader：将图划分为多个子图，每次加载一个子图进行训练。适用于大规模图数据的分布式训练。
  2. GraphSAINTSampler：基于图结构的采样方法，通过随机游走或边采样生成子图，适用于捕捉复杂图结构。
  3. ShaDowKHopSampler：直接采样固定数量跳数的子图，确保每个子图中的节点数量受限，适用于深层消息传递。

1.2 基本用法

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import torch
from torch_geometric.data import Data
from torch_geometric.loader import NeighborLoader

# 节点特征，形状为 [num_nodes, num_features]
x = torch.randn(8, 32)

# 节点标签，形状为 [num_nodes]
y = torch.randint(0, 4, (8, ))

# 边的索引，形状为 [2, num_edges]
edge_index = torch.tensor([
    [2, 3, 3, 4, 5, 6, 7],
    [0, 0, 1, 1, 2, 3, 4]],
)

# 构建图数据
data = Data(x=x, y=y, edge_index=edge_index)

# 初始化 NeighborLoader
loader = NeighborLoader(
    data,
    input_nodes=torch.tensor([0, 1]),  # 初始种子节点
    num_neighbors=[2, 1],  # 每跳采样的邻居节点数
    batch_size=1,   # 批处理大小
    replace=False,  # 不放回采样
    shuffle=False,  # 不打乱种子节点
)

#   0  1
#  / \/ \
# 2  3  4
# |  |  |
# 5  6  7

input_nodes：初始种子节点集合，从这些节点开始进行采样。在这个示例中，初始种子节点是[0, 1]。

num_neighbors：定义每一跳要采样的邻居节点数。在这个示例中，第一跳采样2个邻居，第二跳采样1个邻居。

batch_size：每次采样处理的种子节点数量。在这个示例中，batch_size为1，意味着input_nodes将被分成每次一个节点的小批量进行采样。

replace：是否进行有放回采样。False表示无放回采样，每个邻居节点只能被采样一次。

shuffle：是否在每个epoch中打乱种子节点的顺序。False表示不打乱。

此外，节点和边特征将被过滤为仅包含采样节点/边的特征。

1
2
3
4
5
6
7
8
9
10
11
batch = next(iter(loader))

batch.edge_index
>>> tensor([[1, 2, 3, 4],
            [0, 0, 1, 2]])

 batch.n_id
 >>> tensor([0, 2, 3, 5, 6])

 batch.batch_size
 >>> 1

NeighborLoader从种子节点开始采样，结果子图中的边会指向种子节点。这与PyG的默认消息传递流程（从源节点到目标节点）很好地契合

模型训练

  使用NeighborLoader进行子图采样，使用一个两层的GraphSAGE模型来训练GNN。(对种子节点进行监督学习)

  GraphSAGE（Graph Sample and AggregatE）是一种用于大规模图数据的节点表示学习的模型。它通过采样节点的邻居并聚合邻居的特征来学习节点的表示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from torch_geometric.nn import GraphSAGE
import torch.nn.functional as F
import torch

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

model = GraphSAGE(
    in_channels=32,
    hidden_channels=64,
    out_channels=4,
    num_layers=2
).to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

model = GraphSAGE(...)：定义一个两层的 GraphSAGE 模型。

  • in_channels=32：输入特征的维度是 32。
  • hidden_channels=64：隐藏层特征的维度是 64。
  • out_channels=4：输出特征的维度是 4（通常是类别数）。
  • num_layers=2：使用两层的 GraphSAGE。
  • .to(device)：将模型移动到指定设备（CPU 或 GPU）上。

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)：定义一个 Adam 优化器，用于更新模型参数，学习率设为 0.01。

1
2
3
4
5
6
7
8
9
10
11
12
13
for batch in loader:
    optimizer.zero_grad()
    batch = batch.to(device)
    out = model(batch.x, batch.edge_index)

    # 仅考虑种子节点的预测和标签
    y = batch.y[:batch.batch_size]
    out = out[:batch.batch_size]

    loss = F.cross_entropy(out, y)
    loss.backward()
    optimizer.step()

optimizer.zero_grad()：清除优化器中存储的梯度，确保不累积梯度。

out = model(batch.x, batch.edge_index)：将批次中的节点特征 batch.x 和边索引 batch.edge_index 输入模型，计算输出 out。

y = batch.y[:batch.batch_size]：提取批次中前 batch_size 个种子节点的标签。

out = out[:batch.batch_size]：提取批次中前 batch_size 个种子节点的预测结果。

loss = F.cross_entropy(out, y)：计算交叉熵损失，仅考虑种子节点的预测和标签。

loss.backward()：反向传播计算梯度。

optimizer.step()：使用优化器更新模型参数。

1.3 层次化邻居采样(Hierarchical Extension)

  NeighborLoader 的缺点: 可能会进行无效的计算，造成计算资源的浪费。

  在 GNN 的训练过程中，NeighborLoader 会在每一层采样相应数量的邻居节点。这些采样节点的表示将被用于更新种子节点的表示。然而，在较深的层中采样的邻居节点，其信息可能不再用于更新种子节点的最终表示。例如，在第 3 层中采样的节点，其信息可能在前两层中已经被充分利用，后续层中这些节点的信息不再贡献新的信息。对这些无用节点进行计算是多余的，因为它们的信息不会影响种子节点的最终表示。

  层次化邻居采样就是为了消除这一开销，并进一步加速 mini-batch GNN 的训练。

1.4 高级功能

  NeighborLoader 提供了许多高级功能，以满足不同的使用需求。

同质图和异质图的采样支持

  同质图：所有节点和边都是同一类型。

  异质图：包含不同类型的节点和边。

  对于异质图的采样，只需使用 HeteroData 对象进行初始化。采样异质图时，可以对每种边类型单独指定采样参数，例如为每种边类型单独指定采样的邻居数量。

节省内存的节点合并

  默认情况下，NeighborLoader 将不同种子节点的采样节点融合到一个子图中。这种方式下，共享的邻居节点不会在结果子图中重复，从而节省内存。通过这种方式，可以减少内存消耗。当然也可以通过传递 disjoint=True 选项给 NeighborLoader 来禁用此行为。

有向和双向子图的生成

  默认情况下，从 NeighborLoader 返回的子图将是有向的，这限制了其使用到与采样跳数相等深度的 GNN。

  subgraph_type="bidirectional"：将采样的边转换为双向边，适用于更深层的 GNN。

  subgraph_type="induced"：返回包含所有采样节点的诱导子图。

链接预测的专用采样

  NeighborLoader 主要用于节点级别的采样。LinkNeighborLoader 专为链接预测场景设计,接收一组输入边，进行邻居采样，并返回包含源节点和目标节点的子图。

2. 点云处理 (Point Cloud Processing)

  点云是空间中点的数据集，可以表示三维形状或对象，通常由三维扫描仪获取。点云中的每一个点包含有三维坐标，有些可能含有颜色信息（RGB）或反射强度信息（Intensity）。

image-20240714230048566

  点云默认情况下没有图结构，但我们可以使用PyG的转换工具使其适用于PyG中的全套GNN。关键思想是从点云中创建一个合成图，之后再通过GNN的消息传递方案学习有意义的局部几何结构。然后可以使用这些点的表示来执行点云分类或分割等任务。

2.1 3D点云数据集

  PyG 提供了几个点云数据集，例如 PCPNetDataset、S3DIS 和 ShapeNet 数据集。为了便于学习，教程中以GeometricShapes 数据集为例。这是一个包含各种几何形状（如立方体、球体或金字塔）的玩具数据集。GeometricShapes 数据集默认包含的是网格，而不是点云，通过 pos 和 face 属性表示顶点及其三角连接信息。

加载GeometricShapes 数据集（网格）

1
2
3
4
5
6
7
8
9
from torch_geometric.datasets import GeometricShapes

dataset = GeometricShapes(root='data/GeometricShapes')
print(dataset)
>>> GeometricShapes(40)

data = dataset[0]
print(data)
>>> Data(pos=[32, 3], face=[3, 30], y=[1])

pos 属性：表示网格的顶点坐标。每个顶点有三个坐标值（x, y, z），因此 pos 的形状为 [num_vertices, 3]。pos=[32, 3] 表示这个网格有 32 个顶点，每个顶点由 3 个坐标值表示。

face 属性：表示网格的三角连接信息。每个面（face）由三个顶点索引组成，表示这个三角面是由哪三个顶点构成的。face 的形状为 [3, num_faces]。face=[3, 30] 表示这个网格有 30 个三角面，每个面由三个顶点索引表示。

y 属性：表示标签信息，用于分类任务。y=[1] 表示这个网格有一个标签。

image-20240715000731922

网格转换为点云

  由于我们对点云感兴趣，我们可以通过使用 torch_geometric.transforms 将网格转换为点云。具体来说，PyG 提供了 SamplePoints 转换，该转换将根据面面积均匀采样网格面上的固定数量的点。需要注意的是，采样点是随机的，因此每次访问时都会收到一个新的点云。

1
2
3
4
5
6
7
import torch_geometric.transforms as T

dataset.transform = T.SamplePoints(num=256)

data = dataset[0]
print(data)
# 输出: Data(pos=[256, 3], y=[1])

image-20240715001320125

点云转换为图

  由于我们感兴趣的是学习局部几何结构，我们希望构建一个图形，以便连接附近的点。通常，这可以通过$k$-最近邻搜索或通过球查询（每个点找到在给定半径 $r$ 内的所有邻居）等方式完成。 PyG中的KNNGraph和RadiusGraph转换提供此类图形生成的实用程序。

1
2
3
4
5
6
7
from torch_geometric.transforms import SamplePoints, KNNGraph

dataset.transform = T.Compose([SamplePoints(num=256), KNNGraph(k=6)])

data = dataset[0]
print(data)
>>> Data(pos=[256, 3], edge_index=[2, 1536], y=[1])

  此时，data对象包含edge_index,说明这是一个图，总共有1536条边，256个点。

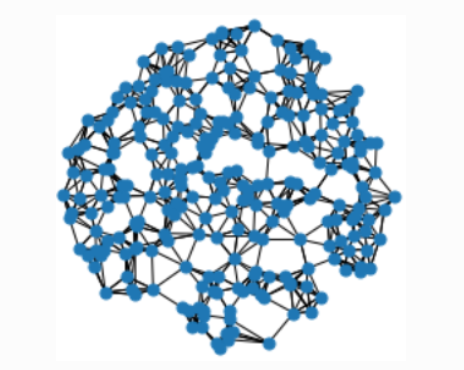
image-20240715002400717

2.2 PointNet++ 实现

  PointNet++提出了一种用于点云分类和分割的图神经网络架构。PointNet++ 通过分组、邻域聚合和下采样迭代地处理点云。

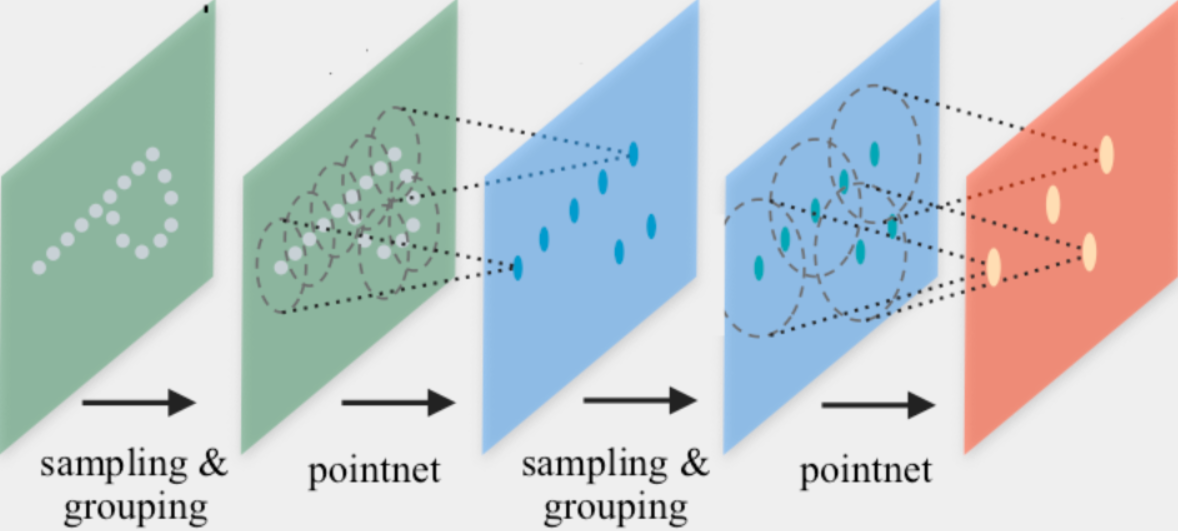
image-20240720004400400

​ 1.分组阶段：通过$k$ -近邻搜索或球查询构建图。

​ 2.邻域聚合阶段：执行 GNN 层，对于每个点，从其直接邻居（由前一阶段构建的图给出）聚合信息。这样，PointNet++ 可以捕获不同尺度的局部上下文。

​ 3.下采样阶段：实现适合具有不同大小点云的池化方案。

领域聚合(Neighborhood Aggregation)

  PointNet++ 定义的简单神经信息传递方案：$h_{i}^{(l+1)}=max_{j∈\mathcal{N}(i)}MLP(h_j^{(l)},p_j−p_i)$

其中：

  • $h_i^{(l+1)}$ 表示在第$l+1$层时点 $i$ 的隐藏特征。
  • $h_j^{(l)}$ 表示在第 $l$ 层时点 $j$ 的隐藏特征。
  • $p_i$和 $p_j$ 分别表示点 $i$ 和点 $j$ 的位置。
  • $\mathcal{N}(i)$ 表示点 $i$的邻域。
  • $\text{MLP}$ 是多层感知器，用于映射邻居点的特征和位置差异。
  • $\max$ 表示在邻域内进行最大池化操作。

  通过使用 PyTorch Geometric (PyG) 的 MessagePassing 接口来实现这一层。这一接口帮助我们自动处理消息传递过程，只需定义消息函数 message() 和聚合方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from torch import Tensor
from torch.nn import Sequential, Linear, ReLU
from torch_geometric.nn import MessagePassing

class PointNetLayer(MessagePassing):
    def __init__(self, in_channels: int, out_channels: int):
        # 使用"max"聚合的消息传递
        super().__init__(aggr='max')

        # 初始化MLP
        # 输入特征维度是隐藏节点维度加上3个位置维度
        self.mlp = Sequential(
            Linear(in_channels + 3, out_channels),
            ReLU(),
            Linear(out_channels, out_channels),
        )

    def forward(self, h: Tensor, pos: Tensor, edge_index: Tensor) -> Tensor:
        # 开始传播消息
        return self.propagate(edge_index, h=h, pos=pos)

    def message(self, h_j: Tensor, pos_j: Tensor, pos_i: Tensor) -> Tensor:
        # h_j: 邻居点的特征 [num_edges, in_channels]
        # pos_j: 邻居点的位置 [num_edges, 3]
        # pos_i: 中心点的位置 [num_edges, 3]

        edge_feat = torch.cat([h_j, pos_j - pos_i], dim=-1)
        return self.mlp(edge_feat)

self.mlp:

  • 初始化一个多层感知器（MLP），用于将邻居点的特征和位置差异映射到新的特征空间。
  • Sequential：按顺序堆叠神经网络层。
  • Linear(in_channels + 3, out_channels)：全连接层，将输入特征（邻居点的特征和位置差异）映射到输出特征。
    • in_channels 是输入特征的维度。
    • +3 是因为每个点有3个位置维度。
  • ReLU()：ReLU激活函数，用于增加模型的非线性能力。
  • Linear(out_channels, out_channels)：再次创建一个全连接层，将前一层的输出特征映射到输出维度。

forward 函数:

  • h：输入特征（每个点的特征）。
  • pos：每个点的位置。
  • edge_index：边索引，定义了图中的连接关系。
  • self.propagate(edge_index, h=h, pos=pos)：调用 propagate 方法开始消息传递,这个方法会自动处理消息计算、消息聚合和节点更新的整个流程。

message 函数:

  • h_j：邻居点的特征。
  • pos_j：邻居点的位置。
  • pos_i：中心点的位置。
  • edge_feat = torch.cat([h_j, pos_j - pos_i], dim=-1)：计算位置差异，并将邻居点的特征和位置差异连接起来。dim=-1 表示沿着最后一个维度进行拼接。h_j 的形状为 [num_edges, in_channels]，pos_j - pos_i 的形状为 [num_edges, 3]，结果张量 edge_feat 的形状为 [num_edges, in_channels + 3]。
  • return self.mlp(edge_feat)：通过 MLP 处理连接后的特征，生成消息。

网络架构(Network Architecture)

  我们可以利用上面的 PointNetLayer 来定义我们的网络架构。(对点云进行学习)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from torch_geometric.nn import global_max_pool


class PointNet(torch.nn.Module):
    def __init__(self):
        super().__init__()

        self.conv1 = PointNetLayer(3, 32)
        self.conv2 = PointNetLayer(32, 32)
        self.classifier = Linear(32, dataset.num_classes)

    def forward(self, pos: Tensor, edge_index: Tensor, batch: Tensor) -> Tensor:
        # 进行两层消息传递
        h = self.conv1(h=pos, pos=pos, edge_index=edge_index)
        h = h.relu()
        h = self.conv2(h=h, pos=pos, edge_index=edge_index)
        h = h.relu()

        # 全局池化
        h = global_max_pool(h, batch)  # [num_examples, hidden_channels]

        # 分类器
        return self.classifier(h)


model = PointNet()
1
2
3
4
5
6
7
print(model)
>>> PointNet(
...   (conv1): PointNetLayer()
...   (conv2): PointNetLayer()
...   (classifier): Linear(in_features=32, out_features=40, bias=True)
... )

构造函数 __init__

  • self.conv1 = PointNetLayer(3, 32)：第一个 PointNet 层，输入特征维度为 3（节点的位置），输出特征维度为 32。
  • self.conv2 = PointNetLayer(32, 32)：第二个 PointNet 层，输入特征维度为 32，输出特征维度为 32。
  • self.classifier = Linear(32, dataset.num_classes)：线性分类器，将 32 维的全局特征映射到数据集的类别数量。

前向传播函数 forward:

  • 第一个 PointNetLayer 将节点的位置特征 pos 转换为 32 维的输出特征，并应用 ReLU 激活函数。

  • 第二个 PointNetLayer 接收第一个层的输出特征并再次转换为 32 维的输出特征，同样应用 ReLU 激活函数。

  • global_max_pool 函数在每个样本的节点维度上取最大值，生成每个点云的全局特征,运行全局池化后，h 的形状会变成 [num_examples, hidden_channels],其中num_examples 表示输入中点云的数量，即点云的个数，hidden_channels 表示每个点云经过特征提取后的特征向量维度，在这个例子中是 32 维。

(classifier): Linear(in_features=32, out_features=40, bias=True)

线性分类器的公式为：

$\text{output} = \text{input} \times \text{weight}^T + \text{bias}$

  • input 是输入特征矩阵，形状为 [batch_size, in_features]，在这里是 [batch_size, 32]。
  • weight 是权重矩阵，形状为 [out_features, in_features]，在这里是 [40, 32]。
  • bias 是偏置向量，形状为 [out_features]，在这里是 [40]。

当 bias=True 时，线性层会在计算输出时添加一个偏置向量，使得每个输出单元都有一个可训练的偏置参数。这可以帮助模型更好地拟合数据，因为偏置项允许每个输出单元在没有输入信号时仍能产生一个激活信号。

  总的来说，这份代码通过继承 torch.nn.Module 创建了我们的网络架构，并在其构造函数中初始化了两个 PointNetLayer 模块和一个最终的线性分类器。

  在 forward() 方法中，我们应用了两个基于图的卷积操作，并通过 ReLU 非线性函数增强它们。第一个操作接收 3 个输入特征（节点的位置），并将它们映射到 32 个输出特征。之后，每个点都包含其二跳邻域的信息，并且应该已经能够区分简单的局部形状。

  接下来，我们应用了一个全局图汇聚函数，即 global_max_pool()，它对每个样本沿节点维度取最大值。为了将不同的节点映射到其对应的样本中，我们使用批次向量，这在使用小批量 torch_geometric.loader.DataLoader 时会自动创建和使用。最后，我们应用一个线性分类器，将每个点云的全局 32 维特征映射到其中的一个类别，该类别属于 40 个可能的类别之一。

训练过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from torch_geometric.loader import DataLoader

# 定义和准备数据集
train_dataset = GeometricShapes(root='data/GeometricShapes', train=True)
train_dataset.transform = T.Compose([SamplePoints(num=256), KNNGraph(k=6)])
test_dataset = GeometricShapes(root='data/GeometricShapes', train=False)
test_dataset.transform = T.Compose([SamplePoints(num=256), KNNGraph(k=6)])

# 创建数据加载器
train_loader = DataLoader(train_dataset, batch_size=10, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=10)

# 初始化 PointNet 模型、优化器和损失函数
model = PointNet()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
criterion = torch.nn.CrossEntropyLoss()

# 训练过程
def train():
    model.train()
    total_loss = 0
    for data in train_loader:
        optimizer.zero_grad()
        logits = model(data.pos, data.edge_index, data.batch)
        loss = criterion(logits, data.y)
        loss.backward()
        optimizer.step()
        total_loss += float(loss) * data.num_graphs
    return total_loss / len(train_loader.dataset)

# 测试过程
@torch.no_grad()
def test():
    model.eval()
    total_correct = 0
    for data in test_loader:
        logits = model(data.pos, data.edge_index, data.batch)
        pred = logits.argmax(dim=-1)
        total_correct += int((pred == data.y).sum())
    return total_correct / len(test_loader.dataset)

# 主训练循环
for epoch in range(1, 51):
    loss = train()
    test_acc = test()
    print(f'Epoch: {epoch:02d}, Loss: {loss:.4f}, Test Acc: {test_acc:.4f}')

创建优化器（Optimizer）:

  • Adam 优化器：torch.optim.Adam 是 PyTorch 中的 Adam 优化器，用于更新神经网络模型的参数，以最小化损失函数。
  • model.parameters()：这个函数会返回模型中所有需要学习的参数。在这里，优化器会使用这些参数来计算梯度并更新它们，使得模型在训练过程中逐渐优化损失函数。
  • 学习率 (lr=0.01)：指定了优化器在每次参数更新时应该采取的步长(学习率)大小。较大的学习率可能会导致快速收敛，但可能会错过最优解；较小的学习率可能会导致收敛速度过慢。选择合适的学习率是训练深度学习模型中的重要考虑因素。

定义损失函数（Loss Criterion）：

  • torch.nn.CrossEntropyLoss() 是交叉熵损失函数，常用于多类别分类问题中计算模型预测值与真实标签之间的差异。
  • 在多类别分类任务中，模型的输出是一个概率分布，交叉熵损失函数衡量了模型预测的概率分布与实际标签的差异程度，越小表示模型预测得越准确。
  • 交叉熵损失函数：对于每个样本，交叉熵损失函数计算预测概率分布与真实概率分布之间的损失，然后求取平均值作为最终的损失值。在神经网络的反向传播过程中，优化器根据这个损失值来调整模型参数，使得模型能够更好地预测出正确的类别。

3.解释图神经网络(Explaining Graph Neural Networks)

  PyTorch Geometric（PyG）从版本2.3开始提供了强大的图神经网络（GNN）解释性功能。这些功能包括：

  1. Explainer类：PyG的Explainer类提供了灵活的接口，能够生成多种类型的解释，帮助理解模型如何基于输入的图数据进行决策或预测。
  2. 解释算法：提供多种解释算法，例如GNNExplainer、PGExplainer和CaptumExplainer。
  3. 可视化支持：支持通过Explanation或HeteroExplanation类可视化解释。
  4. 评估指标：提供metric包中的指标，用于评估解释质量。

3.1 解释器接口(Explainer Interface)

  torch_geometric.explain.Explainer 类为图神经网络（GNN）的解释性提供了一个统一的接口。以下是 Explainer 接口的详细说明：

1. 选择解释算法

  Explainer 类允许用户从 torch_geometric.explain.algorithm 模块中选择一种解释算法。例如，GNNExplainer：通过掩码节点和边来解释GNN模型的预测。

2. 定义解释的类型

  • explanation_type="phenomenon"：解释数据集的底层现象。
  • explanation_type="model"：解释GNN模型的预测。

3. 设置掩码类型

掩码用于确定哪些节点和边对解释是重要的。

  • mask="object"：掩码整个对象。
  • mask="attributes"：掩码对象的特定属性。

4. 掩码后处理

  • threshold_type="topk"：选择前 k 个重要的节点或边。
  • threshold_type="hard"：应用硬阈值以选择重要的节点或边。（只有掩码值超过阈值的节点或边才会被选为重要节点或边）

3.2 示例

解释同质图上的节点分类

  假设已经有一个同构图的数据对象 data 和一个 GNN 模型 model。我们将使用 GNNExplainer 进行解释。使得最终Explanation对象包含 node_mask（表示哪些节点和特征对于预测至关重要）和 edge_mask（表示哪些边对于预测至关重要）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from torch_geometric.data import Data
from torch_geometric.explain import Explainer, GNNExplainer

# 假设已经有一个同构图的数据对象
data = Data(...)

# 创建Explainer实例
explainer = Explainer(
    model=model,
    algorithm=GNNExplainer(epochs=200),
    explanation_type='model',
    node_mask_type='attributes',  # 节点掩码类型为属性掩码
    edge_mask_type='object',      # 边掩码类型为对象掩码
    model_config=dict(
        mode='multiclass_classification',
        task_level='node',
        return_type='log_probs',  # 模型返回对数概率
    ),
)

# 为索引为10的节点生成解释
explanation = explainer(data.x, data.edge_index, index=10)
print(explanation.edge_mask)
print(explanation.node_mask)

  然后，我们可以将特征重要性和解释的关键子图可视化：

1
2
3
4
5
# 可视化特征重要性，选择前10个重要特征
explanation.visualize_feature_importance(top_k=10)

# 可视化解释结果中的子图
explanation.visualize_graph()

  最后，我们可以使用 torch_geometric.explain.metric 模块中的 unfaithfulness 函数对解释结果进行评估。

1
2
3
4
from torch_geometric.explain import unfaithfulness

metric = unfaithfulness(explainer, explanation)
print(metric)

model_config:用于指定模型的详细信息。包含关于模型的操作模式、任务级别和返回类型的配置信息。

  • mode:指定模型的操作模式。multiclass_classification（多类分类任务）、binary_classification（二元分类）和 regression（回归）。
  • task_level:指定任务的级别。node（节点级别的任务）、edge（边级别）、graph（图级别）。
  • return_type ：指定模型返回的输出类型。log_probs（对数概率）、probs（原始概率）、raw（原始未处理的输出值）。

解释异构图上的节点分类

  解释在异构图上进行节点分类的过程可以通过使用 CaptumExplainer 算法结合 IntegratedGradients 归因方法来完成。CaptumExplainer 是对 Captum 库的包装，支持大多数归因方法以解释任何同构或异构的 PyG 模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from torch_geometric.data import HeteroData
from torch_geometric.explain import Explainer, CaptumExplainer
import torch

# 假设已经有一个异构图的数据对象
hetero_data = HeteroData(...)

# 创建Explainer实例
explainer = Explainer(
    model=model,
    algorithm=CaptumExplainer('IntegratedGradients'),  # 使用IntegratedGradients算法
    explanation_type='model',
    node_mask_type='attributes',  # 节点掩码类型为属性掩码
    edge_mask_type='object',      # 边掩码类型为对象掩码
    model_config=dict(
        mode='multiclass_classification',  # 模型进行多类分类
        task_level='node',                 # 节点级别的任务
        return_type='probs',               # 模型返回概率
    ),
)

# 为索引为1和3的节点生成批处理的异构解释
hetero_explanation = explainer(
    hetero_data.x_dict,
    hetero_data.edge_index_dict,
    index=torch.tensor([1, 3]),
)

print(hetero_explanation.edge_mask_dict)
print(hetero_explanation.node_mask_dict)

解释同质图上的图回归

  在同构图上进行图回归任务时，我们可以使用torch_geometric.explain.algorithm.PGExplainer算法生成一个解释。我们将解释器配置为使用edge_mask_type，使最终的Explanation对象包含一个edge_mask（指示哪些边对预测至关重要）。需要哦注意的是，如果向解释器传递node_mask_type，则会抛出错误，因为PGExplainer无法解释节点的重要性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from torch_geometric.data import DataLoader
from torch_geometric.explain import Explainer, PGExplainer

# 假设已经有一个同构图的数据集
dataset = ...
loader = DataLoader(dataset, batch_size=1, shuffle=True)

# 创建Explainer实例
explainer = Explainer(
    model=model,
    algorithm=PGExplainer(epochs=30, lr=0.003),  # 使用PGExplainer算法，指定训练的epochs和学习率
    explanation_type='phenomenon',  # 解释现象，而非模型
    edge_mask_type='object',  # 边掩码类型为对象掩码
    model_config=dict(
        mode='regression',  # 模型进行回归任务
        task_level='graph',  # 图级别的任务
        return_type='raw',  # 模型返回原始值
    ),
    # 仅包含前10个最重要的边
    threshold_config=dict(threshold_type='topk', value=10),
)

# 训练PGExplainer
for epoch in range(30):
    for batch in loader:
        loss = explainer.algorithm.train(
            epoch, model, batch.x, batch.edge_index, target=batch.target)

# 为特定的图生成解释
explanation = explainer(dataset[0].x, dataset[0].edge_index)
print(explanation.edge_mask)

4.浅节点嵌入(Shallow Node Embeddings)

  浅层节点嵌入是一种将图中的节点表示为低维向量的技术。浅层节点嵌入的主要目标是通过一些无监督的学习方法将每个节点嵌入到一个低维空间中，同时保留原始图中的拓扑结构和节点属性信息。通过这种方式，可以在低维空间中进行各种机器学习任务，如节点分类、聚类、链接预测等。

  浅层节点嵌入技术通过浅嵌入查找表将节点嵌入到低维向量表示中，使保留邻域的可能性最大化，即附近的节点应该接收相似的嵌入，而远处的节点应该接收不同的嵌入。

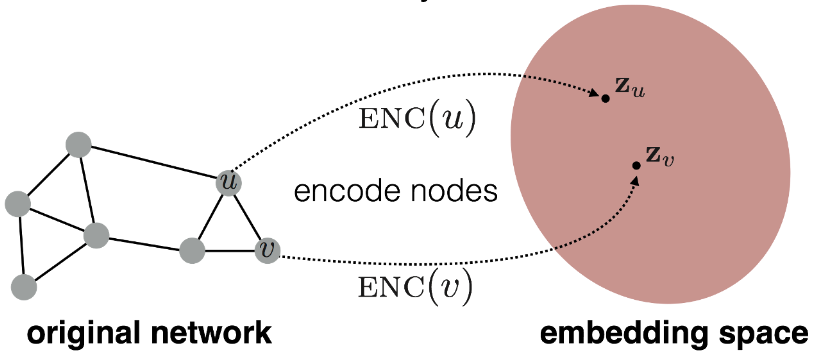
浅节点嵌入

​ 公式 $\text{ENC}(v, G) = Z_v$用于描述节点嵌入的结果。

4.1DeepWalk

  具体来说，给定一个长度为 $k$ 的随机游走 $w=(v_{\Pi(1)}, v_{\Pi(2)}, \ldots, v_{\Pi(k)})$，起始于节点 $v∈V$，其目标是最大化在给定节点 $v$ 的情况下观测到节点 $v_{\Pi(i)}$的可能性。这一目标可以通过在对比学习场景中使用随机梯度下降（SGD）高效地训练。

  损失函数为：

  $L = \sum -\log(\sigma(z_v^T z_{v_{\Pi(i)}})) + \sum -\log(1 - \sigma(z_v^T z_{w’}))$

  其中，非存在的游走（即所谓的负样本）被采样并联合训练， $\sigma$ 表示 Sigmoid 函数。值得注意的是，通常使用嵌入向量间的点积 $z_v^T z_w$ 来衡量相似性，但其他相似性度量也适用。

  重要的是，浅层节点嵌入是以无监督方式进行训练的，最终可以作为给定下游任务的输入。例如，对于节点级别任务，可以直接将节点嵌入$ z_v $用作最终分类器的输入。对于边级别任务，可以通过平均值 $\frac{1}{2}(z_v + z_w)$ 或通过 Hadamard 积 $z_v \cdot z_w$ 获取边级别的表示。

  尽管节点嵌入技术非常简单，但它们也存在一些缺点。特别是，它们无法融入节点和边附带的丰富特征信息，并且由于可学习参数固定于特定图的节点上，无法简单地应用于未见过的图（使这种方法具有归纳性。然而，这种方法仍然是将结构图信息保存在固定大小向量中的常用技术，并且在初始节点特征不丰富的情况下，通常也用于生成 GNN 进一步处理的输入。

  上面的内容是官方文档写的，然鹅，我认为这写的就是一坨，下面是我自己搜索总结的。

  节点 $v$ 是随机游走的起点，也是我们希望学习其嵌入向量$ z_v $的目标节点。随机游走序列$ w = (v_{\Pi(1)}, v_{\Pi(2)}, \ldots, v_{\Pi(k)})$是从节点 $v$ 出发按照一定的随机策略访问的节点序列。我们可以通过生成的序列 $w$ 学习节点 $v$ 的嵌入向量 $z_v$，从而捕捉节点的局部邻域特征和全局结构信息。序列 $ w$ 的生成过程可以通过优化算法（如Skip-gram模型）来提高节点嵌入的质量，使其更好地反映节点在图中的语义和结构位置。

  损失函数 $ L$ 的目的是在 DeepWalk 方法中用来优化节点嵌入向量的学习过程。损失函数 $L$ 通常是通过对比学习（contrastive learning）的方式定义的:

  $L = \sum -\log(\sigma(z_v^T z_{v_{\Pi(i)}})) + \sum -\log(1 - \sigma(z_v^T z_{w’}))$

其中：

  • $z_v$ 是节点 $v$ 的嵌入向量。
  • $z_{v_{\Pi(i)}}$ 是随机游走序列 $w$ 中第 $i$ 步访问到的节点 $v_{\Pi(i)}$ 的嵌入向量。
  • $w’$ 是随机选择的负样本节点的嵌入向量。
  • $\sigma(\cdot)$ 是 Sigmoid 函数，定义为 $\sigma(x) = \frac{1}{1 + e^{-x}}$，用于将相似性度量映射到 (0, 1) 的概率范围内。

  • 正样本项 $-\log(\sigma(z_v^T z_{v_{\Pi(i)}}))$：

    • 正样本项用于最大化节点 $v$ 和其在随机游走序列 $w$ 中访问到的节点 $v_{\Pi(i)}$ 的相似性概率。这部分的优化过程使得在嵌入空间中，节点 $v$ 的嵌入向量 $z_v$ 更接近于其在实际图结构中的邻居节点 $v_{\Pi(i)}$，从而保留了图的局部结构特征。(相似的节点更近)

  • 负样本项 $-\log(1 - \sigma(z_v^T z_{w’}))$：

    • 负样本项用于最小化节点 $v$ 和随机选择的负样本节点 $w’$ 的相似性概率。负样本节点 $w’$ 通常是从未与节点 $v$ 相邻的节点或者通过一定的采样策略选择的其他节点。通过最小化这一项，DeepWalk 强化了节点嵌入向量 $z_v$ 在嵌入空间中与非邻居节点的区分能力。（不相似的节点更远）

  采用梯度下降等优化算法，对损失函数 $L$ 进行优化。通过调整节点 $v$ 的嵌入向量 $z_v$，使得 $L$ 的值最小化或达到收敛，从而学习到节点 $v$ 的最优嵌入表示。

  最终优化得到的节点嵌入向量$ z_v $能够在低维空间中有效地表示节点 $v$ 的结构信息和语义特征。这些嵌入向量可以用于后续的节点分类、链接预测、社区发现等图数据分析任务。

4.2Node2Vec

  Node2Vec 是另一种学习浅层节点嵌入的方法，它是DeepWalk的优化。Node2Vec 方法具有两个重要的参数：

  1. 参数 $p$：参数 $p$ 控制在随机游走过程中立即重新访问节点的概率。具体来说，当 $p > 1$ 时，更倾向于多次访问先前访问过的节点，这种策略有助于捕捉图中的局部结构信息；当 $p<1$ 时，更倾向于向前探索新的节点，有助于扩展搜索空间。
  2. 参数 $q$：参数 $q$ 控制随机游走过程中选择广度优先策略还是深度优先策略。当 $q>1$时，随机游走更倾向于向广度优先策略转变；当 $q<1$ 时，更倾向于向深度优先策略转变。

​

加载数据

1
2
3
from torch_geometric.nn import Node2Vec

data = Planetoid('./data/Planetoid', name='Cora')[0]

初识化Node2Vec模块

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
from torch_geometric.nn import Node2Vec

device = 'cuda' if torch.cuda.is_available() else 'cpu'

model = Node2Vec(
    data.edge_index,
    embedding_dim=128,
    walks_per_node=10,  # 每个节点执行10次随机游走
    walk_length=20,     # 每次随机游走长度为20
    context_size=10,    # 用于梯度优化的随机游走窗口大小
    p=1.0,
    q=1.0,
    num_negative_samples=1, # 每个正样本随机游走生成的负样本数目
).to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

创建数据加载器

1
loader = model.loader(batch_size=128, shuffle=True, num_workers=4) # num_workers表示用于数据加载的工作线程数

生成随机游走

1
pos_rw, neg_rw = next(iter(loader))

  通过迭代加载器获取下一个批次的正样本和负样本随机游走序列。pos_rw包含正随机游走节点索引的张量，形状是 [batch_size * walks_per_node * (2 + walk_length - context_size), context_size]，neg_rw包含负随机游走节点索引的张量，形状是 [num_negative_samples * pos_rw.size(0), context_size]。

模型训练

1
2
3
4
5
6
7
8
9
10
11
12
def train():
    model.train()
    total_loss = 0
    for pos_rw, neg_rw in loader:
        optimizer.zero_grad()
        # 计算正样本和负样本随机游走序列的损失。
        loss = model.loss(pos_rw.to(device), neg_rw.to(device))
        loss.backward()
        optimizer.step()
        # 累计当前批次的损失值
        total_loss += loss.item()
    return total_loss / len(loader)

获取节点嵌入

1
2
z = model()  # 获取所有节点的嵌入向量
z = model(torch.tensor([0, 1, 2]))  # 获取前三个节点的嵌入向量

4.3 MetaPath2Vec

  MetaPath2Vec 是 Node2Vec 的一种扩展，专门用于处理异构图。异构图包含多种类型的节点和边，与传统的同质图不同。在 MetaPath2Vec 中，我们通过元路径（metapath）定义如何在不同类型的节点之间进行随机游走。

  1. 异构图：

    • 包含多种类型的节点和边。例如，在学术网络中，节点可以是作者、论文和期刊，边可以是“写作”、“发表”等。

  2. 元路径（metapath）：

    • 定义了一条特定类型的节点和边之间的路径模式。例如：

      1
      2
      3
      4
      5
      6
      metapath = [
          ('author', 'writes', 'paper'),
          ('paper', 'published_in', 'venue'),
          ('venue', 'publishes', 'paper'),
          ('paper', 'written_by', 'author'),
      ]

    • 这个元路径表示随机游走从作者节点到论文节点，再到期刊节点，然后回到论文节点和作者节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from torch_geometric.nn import MetaPath2Vec

# 假设 edge_index_dict 是一个包含每种边类型的边索引的字典
edge_index_dict = {
    ('author', 'writes', 'paper'): ...,
    ('paper', 'published_in', 'venue'): ...,
    ('venue', 'publishes', 'paper'): ...,
    ('paper', 'written_by', 'author'): ...,
}

# 定义元路径
metapath = [
    ('author', 'writes', 'paper'),
    ('paper', 'published_in', 'venue'),
    ('venue', 'publishes', 'paper'),
    ('paper', 'written_by', 'author'),
]

# 初始化 MetaPath2Vec 模型
model = MetaPath2Vec(
    edge_index_dict=edge_index_dict,
    embedding_dim=128,
    metapath=metapath,
    walks_per_node=10,
    walk_length=20,
    context_size=10,
    num_negative_samples=1,
).to(device)