第136场双周赛 【换根DP】
C. 分类讨论
D. 换根DP
分析:
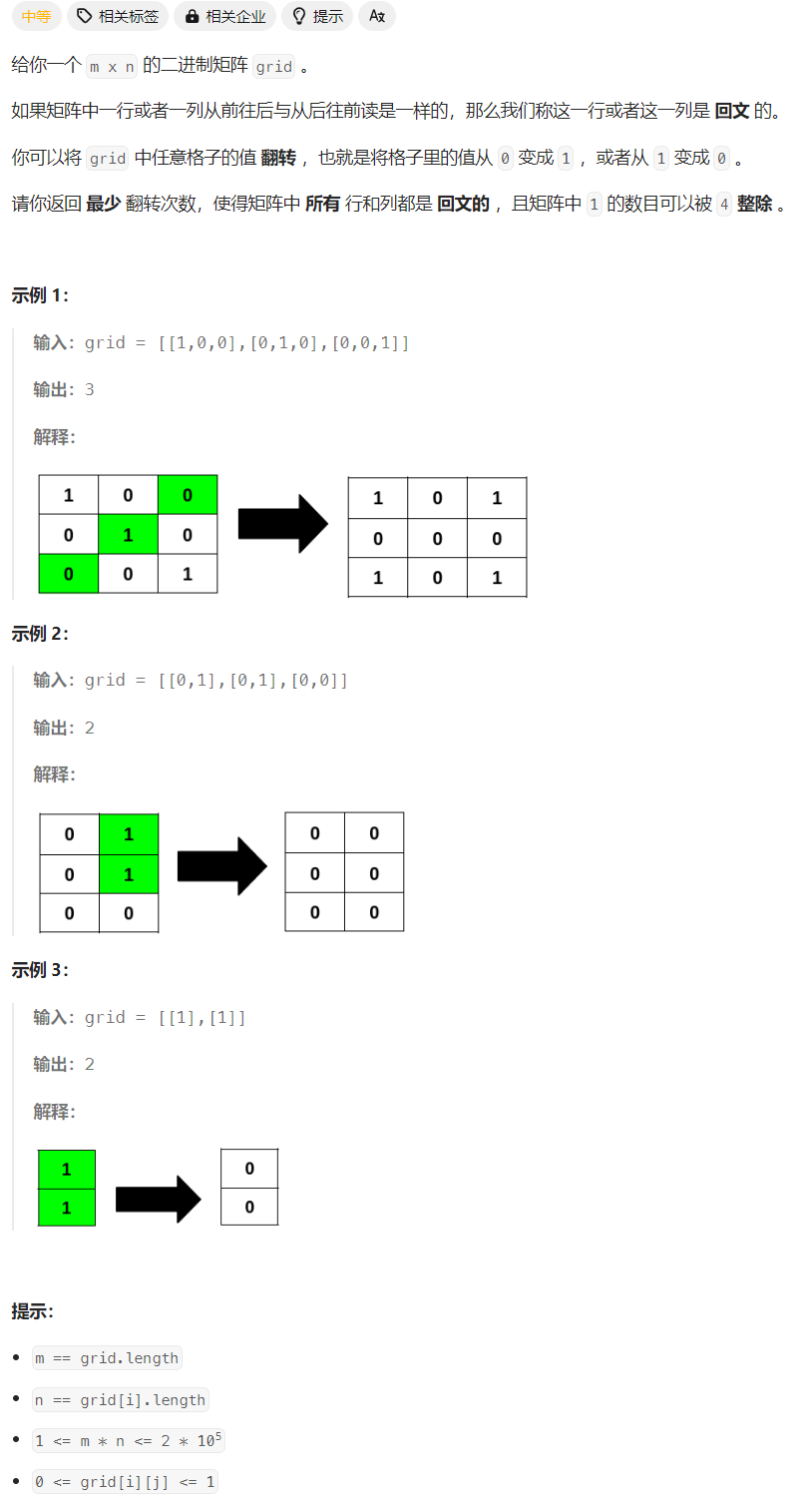
要求行和列都回文。考虑n和m都是偶数的情况下,正好可以把矩阵分成左上、右上、左下、右下四个每部分。任何一个左上的点都在另外三部分有对应的点,那么只要保证回文,1的数量就一定可以被4整除。
对于可能存在的中间一行和一列。首先,如果行和列都是奇数,则正中间的那个数修改为0,因为除了这个点,都是四个一组对应或者是两两对应,如果是1,那么1的总数一定是奇数。其次,对于镜像位置,统计不需要修改的1的数量,记作cnt1,以及有多少位置需要修改,记作sum。最后,分类讨论。
若cnt1 % 4 == 0,则将sum对都修改为0即可;
若cnt1 % 4 == 2,则需要考虑sum,如果sum > 0,则只需要把其中一对改成1,剩下的都改成0即可。如果sum == 0,则需要额外把cnt1中的两个1改成0。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
int minFlips(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
int num1, ans = 0;
for(int i = 0; i < n / 2; ++i)
{
for(int j = 0; j < m / 2; ++j)
{
num1 = grid[i][j] + grid[n - i - 1][j] + grid[i][m - j - 1] + grid[n - i - 1][m - j - 1];
ans += min(num1, 4 - num1);
}
}
if(n % 2 && m % 2) ans += grid[n / 2][m / 2];
int cnt1 = 0, sum = 0;
if(n&1)
{
for(int j = 0; j < m / 2; ++j)
{
if(grid[n / 2][j] == grid[n / 2][m - j - 1]) cnt1 += grid[n / 2][j] * 2;
else ++sum;
}
}
if(m&1)
{
for(int i = 0; i < n / 2; ++i)
{
if(grid[i][m / 2] == grid[n - i - 1][m / 2]) cnt1 += grid[i][m / 2] * 2;
else ++sum;
}
}
return ans + (sum ? sum : cnt1 % 4);
}
};
|
分析:
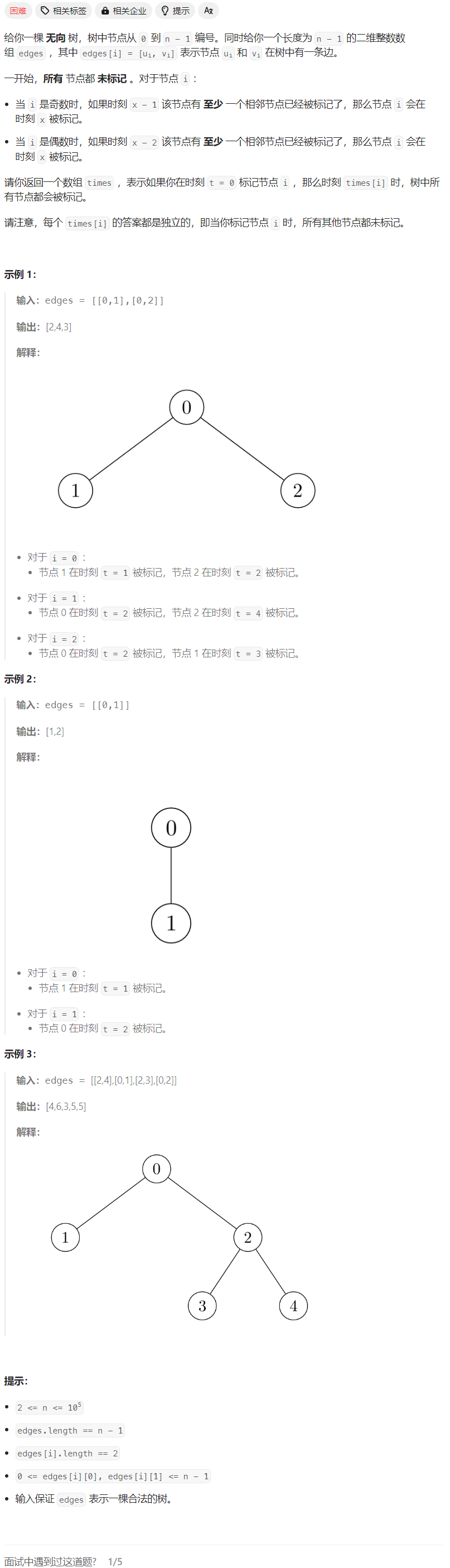
首先,搞明白这题的本质。即有一颗n个节点,2n-2条边的有向树,边权与边的终点的奇偶性有关。求ans[i],表示以i为根节点时,树的最大深度是多少。
暴力的方法是进行n次DFS,正解是换根DP。
我们可以先以节点0为根节点进行一次DFS。在此期间,对于每个节点y维护一个三元组[mx1, mx2, mx_node],表示以节点y为根的子树的最大深度、次大深度、最大深度子树的根节点。之后在第二个DFS中求解ans[i]。假设节点x是y的父节点,当我们需要求ans[y]时,我们考虑把树看成一颗以y为根节点的树,此时树的最大深度与y的所有子树有关,而我们在第一次DFS时维护了考虑除了以x为根节点的所有子树的情况下的最大深度,即y的mx1,记作ans1。那么ans[y]只需要将ans1和以x为根节点的子树的最大深度(记作ans2)取max。
视频讲解(b站 灵茶山艾府)
关于代码,我的代码在第二次DFS中会修改节点对应的三元组,我认为比较便于理解换根的过程(DFS到节点x时会计算其儿子y的答案)。还有一种写法是在DFS的过程中维护从当前节点y的父节点x出发,向上走的最大深度from_up,这样也非常方便答案的更新,在这种方法下,我们始终将树看成以0为根节点(DFS到节点x时计算x的答案)。
对于from_up的更新,如果x 的儿子 y = mx_node,那么DFS到y时,form_up应该修改为
$max(fromup, mx2) + 2 - x \% 2$,如果y! = mx_node,则应该修改为$max(fromup, mx1) + 2 - x \% 2$。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| class Solution {
public:
vector<int> timeTaken(vector<vector<int>>& edges) {
vector<vector<int>> vt(edges.size() + 1);
for(auto x: edges)
{
int u = x[0], v = x[1];
vt[u].push_back(v);
vt[v].push_back(u);
}
vector<tuple<int, int, int>> nodes(vt.size());
function<int(int, int)> dfs = [&](int x, int fa)
{
int mx1 = 0, mx2 = 0, mx_node = 0;
for(int y: vt[x])
{
if(y == fa) continue;
int dep = dfs(y, x) + 2 - y % 2;
if(dep > mx1)
{
mx2 = mx1;
mx1 = dep;
mx_node = y;
}
else if(dep > mx2) mx2 = dep;
}
nodes[x] = {mx1, mx2, mx_node};
return mx1;
};
vector<int> ans(vt.size());
ans[0] = dfs(0, -1);
function<void(int, int)> ddfs = [&](int x, int fa)
{
int mx1, mx2, mx_node;
int ans1, ans2;
for(int y: vt[x])
{
if(y == fa) continue;
mx1 = get<0>(nodes[y]), mx2 = get<1>(nodes[y]), mx_node = get<2>(nodes[y]);
if(y == get<2>(nodes[x]))
{
ans1 = mx1, ans2 = get<1>(nodes[x]) + 2 - x % 2;
ans[y] = max(ans1, ans2);
}
else
{
ans1 = mx1, ans2 = get<0>(nodes[x]) + 2 - x % 2;
ans[y] = max(ans1, ans2);
}
if(ans2 > mx1)
{
mx2 = mx1;
mx1 = ans2;
mx_node = x;
}
else if(ans2 > mx2) mx2 = ans2;
nodes[y] = {mx1, mx2, mx_node};
ddfs(y, x);
}
};
ddfs(0, -1);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public:
vector<int> timeTaken(vector<vector<int>>& edges) {
vector<vector<int>> vt(edges.size() + 1);
for(auto x: edges)
{
int u = x[0], v = x[1];
vt[u].push_back(v);
vt[v].push_back(u);
}
vector<tuple<int, int, int>> nodes(vt.size());
function<int(int, int)> dfs = [&](int x, int fa)
{
int mx1 = 0, mx2 = 0, mx_node = 0;
for(int y: vt[x])
{
if(y == fa) continue;
int dep = dfs(y, x) + 2 - y % 2;
if(dep > mx1)
{
mx2 = mx1;
mx1 = dep;
mx_node = y;
}
else if(dep > mx2) mx2 = dep;
}
nodes[x] = {mx1, mx2, mx_node};
return mx1;
};
dfs(0, -1);
vector<int> ans(vt.size());
function<void(int, int, int)> ddfs = [&](int x, int fa, int from_up)
{
auto& [mx1, mx2, mx_node] = nodes[x];
ans[x] = max(from_up, mx1);
for(int y: vt[x])
{
if(y == fa) continue;
ddfs(y, x, max(from_up, (y == mx_node ? mx2 : mx1)) + 2 - x % 2);
}
};
ddfs(0, -1, 0);
return ans;
}
};
|

