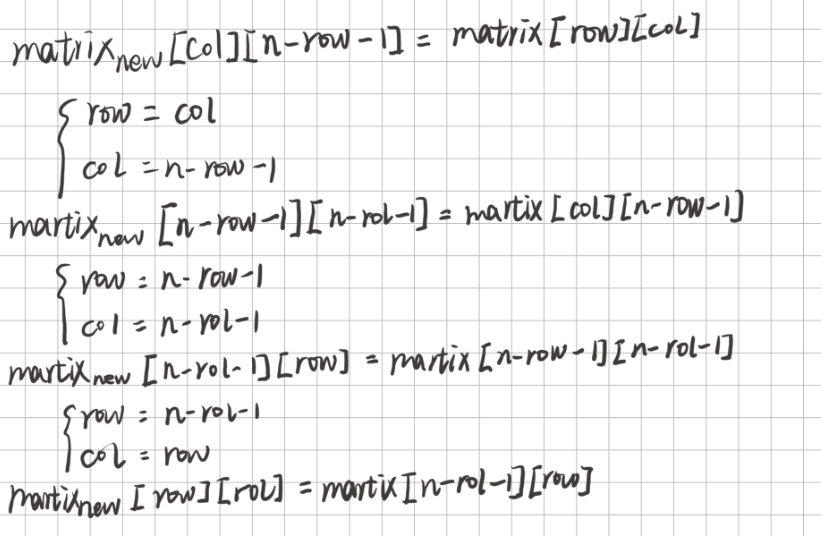leetcode 热题 100
C/C++ 版本
[TOC]
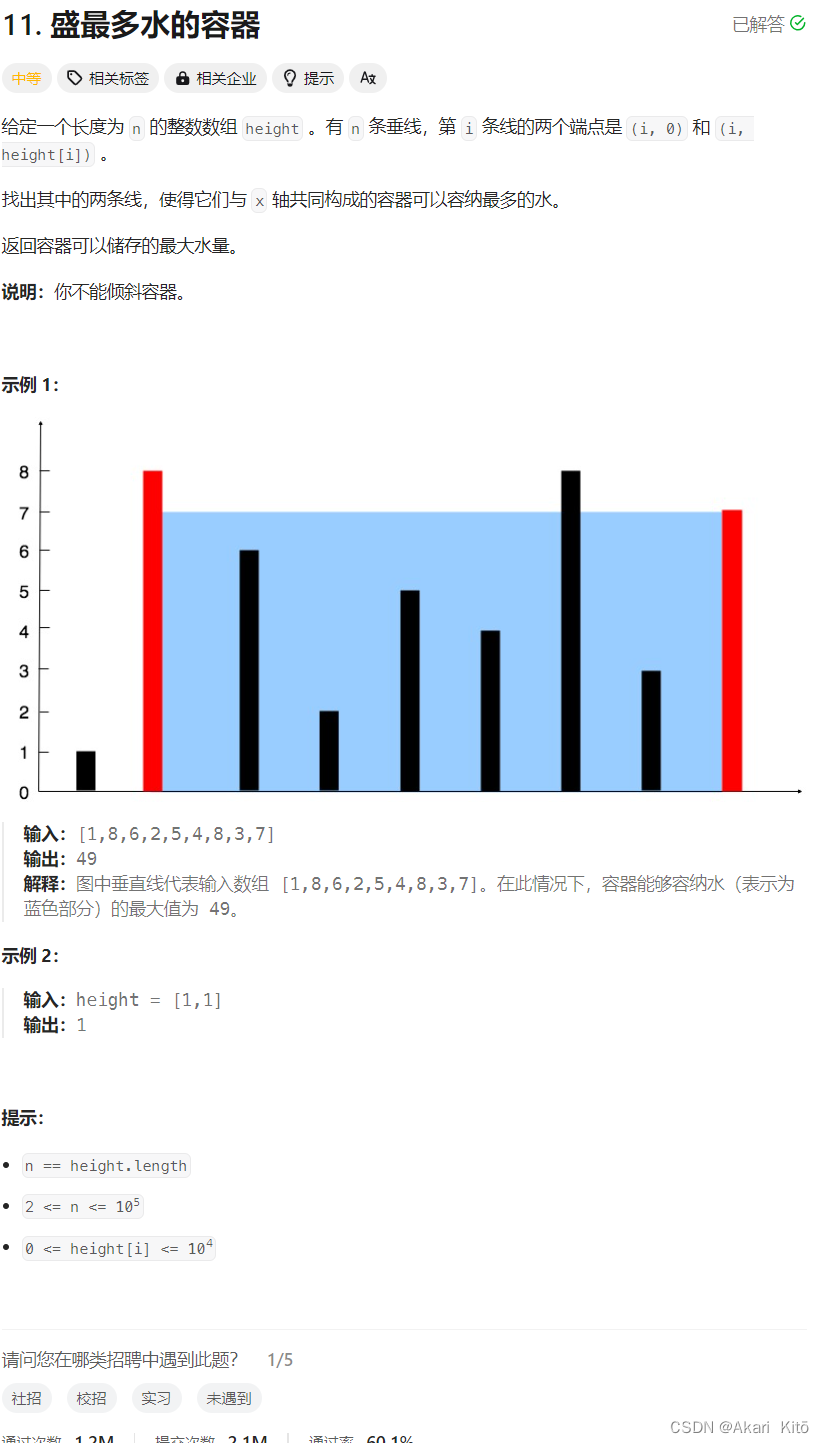
双指针 思路: i,j,初始时i,j都位于左界附近,但是对于第i次的内层循环,j只需要从第i-1次内层循环停下时的j开始循环,即内层的循环变量j一直在增加,而不会减少,故双指针复杂度O(n)。l,r,初始分别位于左界和右界,之后++l和--r,这样子移动。V=(r - l - 1) * min(height[l], height[r])。为取得Vmax,考虑无论移动l or r,都会使得宽d = r - l - 1变小,故考虑如何使得min(height[l], height[r])变大,容易发现应该移动height小的那一个。AC代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : int maxArea (vector<int >& height) int n = height.size (); int l = 0 , r = n - 1 ; int s = (r - l) * min (height[l], height[r]); int res = s; while (l < r) { if (height[l] < height[r]) ++l; else --r; s = (r - l) * min (height[l], height[r]); res = max (res, s); } return res; } };
思路: nums[i],需要从右边找出两个数字使得和为-nums[i]。l,r初始分别为左界和右界,据nums[l] + nums[r]与-nums[i]的大小关系决定移动哪个指针即可。set逃课。AC代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution {public : vector<vector<int >> threeSum (vector<int >& nums) { int n = nums.size (); vector<vector<int >> res; set<vector<int >> st; sort (nums.begin (), nums.end ()); int a, sum, last = -5000000 ; int l, r; bool flag; for (int i = 0 ; i < n; ++i) { if (nums[i] == last) continue ; else { last = nums[i]; l = i + 1 ; r = n - 1 ; a = -nums[i]; while (l < r) { sum = nums[l] + nums[r]; if (sum > a) --r; else if (sum < a) ++l; else { vector<int > vt; vt.push_back (nums[i]); vt.push_back (nums[l]); vt.push_back (nums[r]); st.insert (vt); ++l; } } } } for (auto x : st) res.push_back (x); return res; } };
Updated on 2024_12_03
分析:
去重方面不使用set逃课。主要有两点,对于第一个元素,如果当前第一个元素等于前一个元素,那么直接continue,这涉及到一个子集的问题。第二点就是对于第二个元素,即将答案放入之后,左指针的移动,不能只移动一位,要移动到右侧第一个不等于当前这次答案里的第二个元素的那个点上。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution {public : vector<vector<int >> threeSum (vector<int >& nums) { int n = nums.size (); sort (nums.begin (), nums.end ()); vector<vector<int >> ans; const int inf = 0x3f3f3f3f ; int x, y, l, r, last; for (int i = 0 ; i < n; ++i) { if (i != 0 && nums[i] == nums[i - 1 ]) continue ; x = nums[i]; y = -nums[i]; l = i + 1 ; r = n - 1 ; last = inf; while (l < r) { if (nums[l] + nums[r] == y) { ans.push_back ({nums[i], nums[l], nums[r]}); last = nums[l]; while (nums[++l] == last && l != n - 1 ) ; } else if (nums[l] + nums[r] < y) ++l; else --r; } } return ans; } };
思路: l,r初始分别为左界右界,移动过程中,分别维护扫过区域的最大值,每次移动最大值较小的那一侧,然后判断移动之后是洼地还是高地,洼地则计算接的雨水,高地则更新单侧最大值。r。r侧,由于移动之后可能是高地or洼地,对于高地,不计算贡献,其实无所谓,但是对于洼地,需要计算贡献,此时贡献取决于洼地两侧最高的高地的较小值,然而左侧最高的高地其实是不确定的,故无法计算。倘若移动是l的一侧,虽然右侧最高的高地也是不确定的,但至少可以确定的是右侧的高地一定比左侧的高,故可以计算正确的贡献。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int trap (vector<int >& height) int n = height.size (); vector<int > rmx (n, 0 ) ; rmx[n - 1 ] = height[n - 1 ]; for (int i = n - 2 ; i >= 0 ; --i) rmx[i] = max (height[i], rmx[i + 1 ]); int lmx = height[0 ], ans = 0 ; for (int i = 1 ; i < n - 1 ; ++i) { ans += max (min (lmx, rmx[i + 1 ]) - height[i], 0 ); lmx = max (lmx, height[i]); } return ans; } };
双指针:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : int trap (vector<int >& height) int n = height.size (); int res = 0 ; int l = 0 , r = n - 1 ; int lmx = height[0 ], rmx = height[n - 1 ]; while (l < r) { if (lmx < rmx) { ++l; if (lmx > height[l]) res += lmx - height[l]; else lmx = height[l]; } else { --r; if (rmx > height[r]) res += rmx - height[r]; else rmx = height[r]; } } return res; } };
单调栈:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution {public : int trap (vector<int >& height) stack<int > st; int n = height.size (); int res = 0 ; for (int i = 0 ; i < n; ++i) { while (!st.empty () && height[i] > height[st.top ()]) { int tp = st.top (); st.pop (); if (st.empty ()) break ; int l = st.top (); int d = i - l - 1 ; int h = min (height[l], height[i]) - height[tp]; res += d * h; } st.push (i); } return res; } };
子串 思路: s的左边界且能覆盖t的最小子串。l,r++l,否则++r,每次移动后判断新的子串是否能够覆盖并且是否变小,保存最小能覆盖的子串长度以及其左右边界l,r。
1 2 3 4 5 6 map<char , int > mp; int cnt_s[64 ] int cnt_t [64 ]; int num = 0 , cnt = 0 ; int l, r; int min_l, min_r, mi = inf;
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 class Solution {public : string minWindow (string s, string t) { const int inf = 0x3f3f3f3f ; int len1 = s.size (), len2 = t.size (); map<char , int > mp; int cnt_s[64 ], cnt_t [64 ]; int num = 0 , cnt = 0 ; int l, r, min_l = 0 , min_r = 0 , mi = inf; string str; for (char ch = 'a' ; ch <= 'z' ; ++ch) mp[ch] = ch - 'a' + 1 ; for (char ch = 'A' ; ch <= 'Z' ; ++ch) mp[ch] = ch - 'A' + 1 + 26 ; for (int i = 0 ; i < len2; ++i) ++cnt_t [mp[t[i]]]; for (int i = 1 ; i < 55 ; ++i) if (cnt_t [i]) ++num; l = 0 , r = -1 ; while (r < len1) { if (cnt == num) { if (cnt_s[mp[s[l]]] == cnt_t [mp[s[l]]]) --cnt; --cnt_s[mp[s[l++]]]; } else { ++cnt_s[mp[s[++r]]]; if (cnt_s[mp[s[r]]] == cnt_t [mp[s[r]]]) ++cnt; } if (cnt == num && r - l + 1 < mi) { mi = r - l + 1 ; min_l = l, min_r = r; } } if (mi == inf) return "" ; else { str = s.substr (min_l, mi); return str; } } };
普通数组 思路 O(1),且不用reverse的方法。(官方题解推导比较清楚)。pos和tmp,分别表示现在的位置和对应位置上的值,由此,更新只需pos = (pos + k) % n,swap(nums[pos], tmp),当pos回到最开始的位置时,我们称这是完成了一趟修改,此时应该停下,然鹅有的元素并没有遍历到。(只将下标为gcd(k,n)的倍数的元素遍历了,可证,另见类似题目,2015ICPC沈阳,跳青蛙🐸容斥 ),故需要将pos+1,再依次为开始,继续上述操作,直至回到开始位置并遍历全部位置。gcd(n,k)趟)。假设转了a圈,遍历了b个元素,则an=bk,故an一定是n,k的倍数,又因为我们在第一次回到起点时便结束了,故a应尽可能的小,由此an=lcm(n,k),故b=lcm(n,k)/k,即需要遍历的趟数cnt=n/b=gcd(n,k)。AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : int gcd (int a, int b) { return b == 0 ? a : gcd (b, a % b); } void rotate (vector<int >& nums, int k) int n = nums.size (); k %= n; int cnt = gcd (n, k); for (int i = 0 ; i < cnt; ++i) { int pos = i; int tmp = nums[i]; while (true ) { pos = (pos + k) % n; swap (nums[pos], tmp); if (pos == i) break ; } } } };
思路:
对nums[i]<=0||nums[i]>n的元素统一处理。(设置为较大值或数组中出现过的某个1~n的值)。
对于x = nums[i],考虑swap(nums[i], nums[x-1]),即将nums[i]放到他应该在的位置上,如此循环下去,但是注意到当nums[i] == nums[x-1]时会进入死循环。
所有1~n之间的数字都应当被放到对应的位置上,故最后遍历一遍数组,找到第一个不在对应位置之上的元素,便可知答案。bool型数组,需要空间复杂度O(n),原始数组nums同时充当bool数组(原地哈希)bool数组的方法,开一个大小为n+5的bool数组flag,flag[i]=true表示i出现,为此只需要找第一个flag[i]==false的i即可。
同方法1。
通过第一步nums数组中应当只有正数。此时,对于一个1~n之间的数字x,我们就将nums[x - 1]中的元素修改为-nums[x - 1](主要不要多次修改,以防负负得正)。即nums数组中元素的正负代表上述bool型数组的true和false,绝对值代表对应元素的值。
与方法1类似。
AC代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : int firstMissingPositive (vector<int >& nums) { int n = nums.size (); for (int i = 0 ; i < n; ++i) while (nums[i] > 0 && nums[i] <= n && nums[i] != nums[nums[i] - 1 ]) swap (nums[i], nums[nums[i] - 1 ]); for (int i = 0 ; i < n; ++i) if (nums[i] != i + 1 ) return i + 1 ; return n + 1 ; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : int firstMissingPositive (vector<int >& nums) { int n = nums.size (); int x; bool flag = false ; for (auto x: nums) if (x == 1 ) flag = true ; if (!flag) return 1 ; for (int i = 0 ; i < n; ++i) if (nums[i] <= 0 || nums[i] > n) nums[i] = 1 ; for (int i = 0 ; i < n; ++i) { x = abs (nums[i]) - 1 ; nums[x] = -abs (nums[x]); } for (int i = 0 ; i < n; ++i) if (nums[i] > 0 ) return i + 1 ; return n + 1 ; } };
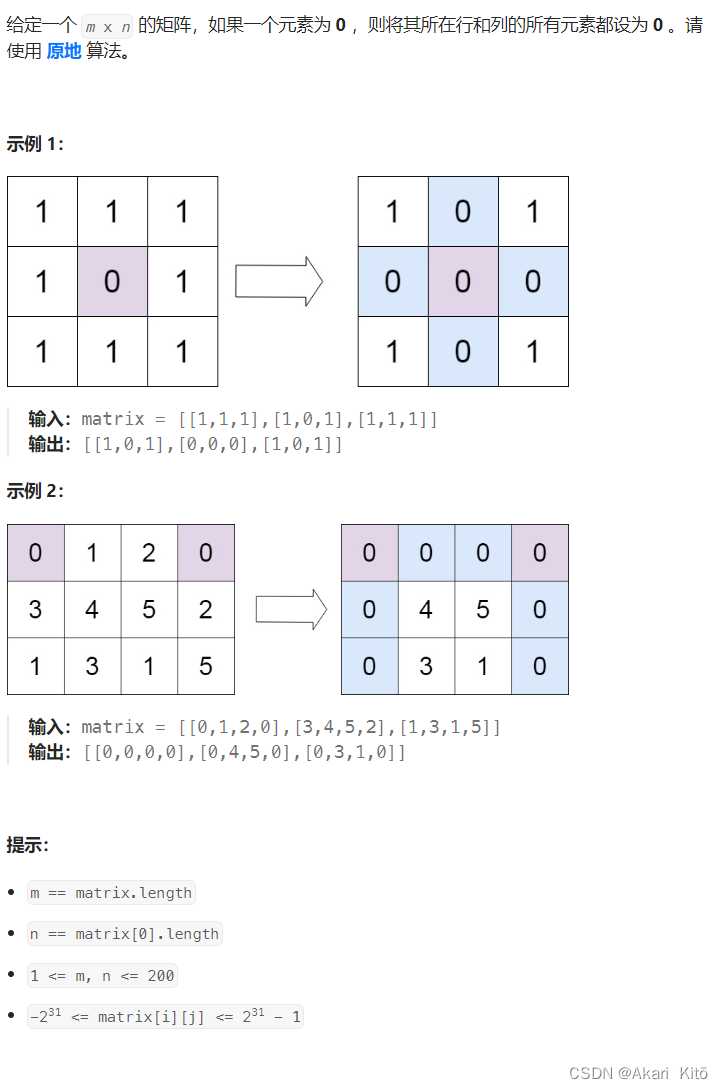
矩阵 思路: n和长度为m的bool型数组,分别表示第i行和第j列是否有0。这样空间复杂度O(n+m)。优化方法是用原数组的第一行和第一列充当这个bool数组。bool型变量col和row表示第1列,第1行是否有0,之后对于matrix[i][j]==0,将matrix[i][0]和matrix[0][i]标记为00所在的行和列全部置为0,后来的出现0不会操作。容易想到的一个思路就是先把有0的行和列中不是0的数字置为一个奇怪的数字(比如inf或是-inf),最后再把这些数改为0,但是发现取值为int的最小值到最大值,所以不行。但是n,m最大为200,随机生成的一个int在矩阵中出现的概率极低,故我们随机生成一个数字作为上述中的奇怪数字即可。(当然是需要判断的,如果运气不好,随机生成的数字正好出现了,就再随机生成一个)
AC代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 class Solution {public : void setZeroes (vector<vector<int >>& matrix) int n = matrix.size (); int m = matrix[0 ].size (); bool col = false , row = false ; for (int i = 0 ; i < n; ++i) { if (!matrix[i][0 ]) { col = true ; break ; } } for (int i = 0 ; i < m; ++i) { if (!matrix[0 ][i]) { row = true ; break ; } } for (int i = 1 ; i < n; ++i) { for (int j = 1 ; j < m; ++j) { if (!matrix[i][j]) matrix[i][0 ] = matrix[0 ][j] = 0 ; } } for (int i = 1 ; i < n; ++i) { for (int j = 1 ; j < m; ++j) { if (!matrix[i][0 ] || !matrix[0 ][j]) matrix[i][j] = 0 ; } } if (col) for (int i = 0 ; i < n; ++i) matrix[i][0 ] = 0 ; if (row) for (int i = 0 ; i < m; ++i) matrix[0 ][i] = 0 ; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class Solution {public : int st_rand (vector<vector<int >>& matrix) { int xx = matrix.size (); int yy = matrix[0 ].size (); srand (time (NULL )); int st; bool flag; while (true ) { st = rand (); flag = false ; for (int i = 0 ; i < xx; ++i) { for (int j = 0 ; j < yy; ++j) { if (matrix[i][j] == st) { flag = true ; break ; } } if (flag) break ; } return st; } } void work (vector<vector<int >>& matrix, int x, int y, int st) { int xx = matrix.size (); int yy = matrix[0 ].size (); for (int i = 0 ; i < xx; ++i) if (matrix[i][y] != 0 ) matrix[i][y] = st; for (int i = 0 ; i < yy; ++i) if (matrix[x][i] != 0 ) matrix[x][i] = st; } void setZeroes (vector<vector<int >>& matrix) int xx = matrix.size (); int yy = matrix[0 ].size (); int st = st_rand (matrix); for (int i = 0 ; i < xx; ++i) { for (int j = 0 ; j < yy; ++j) { if (matrix[i][j] == 0 ) work (matrix, i, j, st); } } for (int i = 0 ; i < xx; ++i) { for (int j = 0 ; j < yy; ++j) { if (matrix[i][j] == st) matrix[i][j] = 0 ; } } } };
分析:
关键在于如何原地 实现,数学公式推导是重点。官方题解很详细。
官方题解方法二原地旋转是重点。
以及与方法三相关的各种翻转方法。(本质还是方法二中的公式)
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class Solution {public : void rotate (vector<vector<int >>& matrix) int n = matrix.size (); int m = n / 2 ; int row, col, n_row, n_col, tmp, temp; for (int i = 0 ; i < m; ++i) { for (int j = 0 ; j < m; ++j) { row = i, col = j; tmp = matrix[row][col]; for (int k = 0 ; k < 4 ; ++k) { n_row = col, n_col = n - row - 1 ; temp = matrix[n_row][n_col]; matrix[n_row][n_col] = tmp; tmp = temp; row = n_row; col = n_col; } } } if (n&1 ) { for (int i = 0 ; i < m; ++i) { row = m, col = i; tmp = matrix[row][col]; for (int k = 0 ; k < 4 ; ++k) { n_row = col, n_col = n - row - 1 ; temp = matrix[n_row][n_col]; matrix[n_row][n_col] = tmp; tmp = temp; row = n_row; col = n_col; } } } } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : void rotate (vector<vector<int >>& matrix) int n = matrix.size (); int m = n / 2 ; for (int i = 0 ; i < n; ++i) reverse (matrix[i].begin (), matrix[i].end ()); for (int i = 0 ; i < n; ++i) { for (int j = 0 ; j < n - i; ++j) swap (matrix[i][j], matrix[n - 1 - j][n - 1 - i]); } } };
分析:
根据矩阵的性质,从右上角开始遍历。若右上角元素小于target,说明当前这一行都不可能是答案,若大于则当前一列都不可能是。复杂度O(m+n)。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : bool searchMatrix (vector<vector<int >>& matrix, int target) int n = matrix.size (); int m = matrix[0 ].size (); int i = 0 , j = m - 1 ; while (i < n && j >= 0 ) { if (matrix[i][j] == target) return true ; else if (matrix[i][j] < target) ++i; else --j; } return false ; } };
链表 分析:
先用快慢指针 寻找链表的中间结点。然后反转链表后半部分,之后遍历两个链表即可。
快慢指针 :快指针一次跳两个节点,慢指针一次跳一个节点。
找中间节点 和反转链表 这两部分的函数感觉可以当模板 。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 class Solution {public : ListNode* findMid (ListNode* head) { ListNode* fast = head; ListNode* slow = head; while (fast != nullptr ) { fast = fast->next; if (fast != nullptr ) fast = fast->next; slow = slow->next; } return slow; } ListNode* reverseList (ListNode* head) { ListNode* pre = nullptr ; ListNode* cur = head; ListNode* nextTemp = nullptr ; while (cur != nullptr ) { nextTemp = cur->next; cur->next = pre; pre = cur; cur = nextTemp; } return pre; } bool isPalindrome (ListNode* head) if (head == nullptr ) return true ; ListNode* midNode = findMid (head); midNode = reverseList (midNode); ListNode* p1 = head; ListNode* p2 = midNode; while (p2 != nullptr ) { if (p1->val != p2->val) return false ; p1 = p1->next; p2 = p2->next; } return true ; } };
好难的题。占位符,以后再写。
分析:
easy的难度,但是哥们写的不太顺利呀。方法一,直接递归,想一下这个问题的子问题,你就会发现这个问题很符合递归。方法二,迭代,记得定义一个头节点,会方便处理很多。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution {public : ListNode* mergeTwoLists (ListNode* list1, ListNode* list2) { if (list1 == nullptr ) return list2; else if (list2 == nullptr ) return list1; else if (list1->val <= list2->val) { list1->next = mergeTwoLists (list1->next, list2); return list1; } else { list2->next = mergeTwoLists (list1, list2->next); return list2; } } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : ListNode* mergeTwoLists (ListNode* list1, ListNode* list2) { ListNode* head = new ListNode (-1 ); ListNode* pre = head; while (list1 != nullptr && list2 != nullptr ) { if (list1->val <= list2->val) { pre->next = list1; list1 = list1->next; } else { pre->next = list2; list2 = list2->next; } pre = pre->next; } pre->next = list1 == nullptr ? list2 : list1; return head->next; } };
分析:
又是一个很符合递归特征的题目。递归+迭代两种解法。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2, int carry = 0 ) { if (l1 == nullptr && l2 == nullptr ) return carry ? new ListNode (carry) : nullptr ; if (l1 == nullptr ) swap (l1, l2); int sum = carry + l1->val + (l2 ? l2->val : 0 ); l1->val = sum % 10 ; l1->next = addTwoNumbers (l1->next, (l2 ? l2->next : nullptr ), sum / 10 ); return l1; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution {public : ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) { ListNode head; ListNode* cur = &head; int carry = 0 ; while (l1 || l2 || carry) { if (l1) { carry += l1->val; l1 = l1->next; } if (l2) { carry += l2->val; l2 = l2->next; } cur = cur->next = new ListNode (carry % 10 ); carry /= 10 ; } return head.next; } };
分析:
前指针在后指针的前面n个节点即可。然后同时向前移动,这样前指针到链表尾的时候,后指针的next正好书倒数第N个节点,但是有个问题就是前后指针其实横跨了n+1个节点。所以,如果n=链表长度的话,会出错,这时候只需要添加一个哨兵节点(头节点)即可。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : ListNode* removeNthFromEnd (ListNode* head, int n) { ListNode dummy{0 , head}; ListNode* left = &dummy; ListNode* right = &dummy; while (n--) right = right -> next; while (right->next != nullptr ) { left = left->next; right = right->next; } ListNode* nxt = left->next; left->next = left->next->next; delete nxt; return dummy.next; } };
分析:
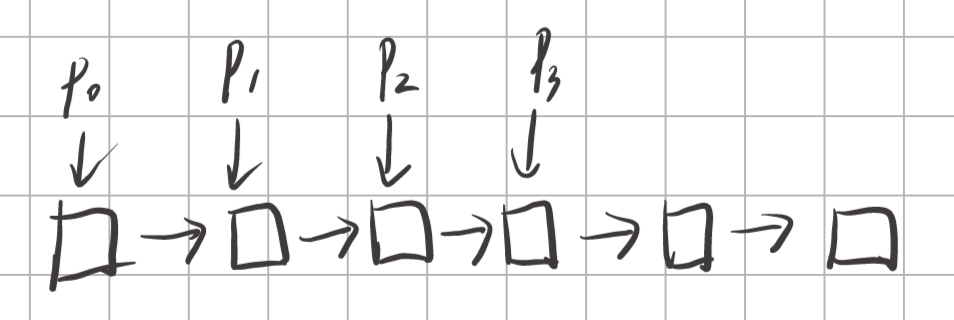
如图,需要反转的是p1和p2,维护好这四个变量即可。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : ListNode* swapPairs (ListNode* head) { ListNode dummy{0 , head}; ListNode* p0 = &dummy; ListNode* p1 = head; ListNode* p2 = nullptr ; ListNode* p3 = nullptr ; while (p1 != nullptr && p1->next != nullptr ) { p2 = p1->next; p3 = p2->next; p2->next = p1; p0->next = p2; p1->next = p3; p0 = p1; p1 = p3; } return dummy.next; } };
分析:
单纯只考虑next指针,不考虑random指针,如下图。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class Solution {public : Node* copyRandomList (Node* head) { Node* p = head; while (p) { Node* copy = new Node (p->val); copy->next = p->next; p->next = copy; p = copy->next; } p = head; while (p) { if (p->random) p->next->random = p->random->next; p = p->next->next; } Node* dummy = new Node (0 ); Node* q = dummy; p = head; while (p) { q->next = p->next; q = q->next; p->next = q->next; p = p->next; } return dummy->next; } };
分析:
归并排序。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 class Solution {public : ListNode* sortList (ListNode* head) { if (head == nullptr || head->next == nullptr ) { return head; } ListNode* mid = findmid (head); ListNode* left = sortList (head); ListNode* right = sortList (mid); return merge (left, right); } private : ListNode* findmid (ListNode* head) { ListNode* slow = head; ListNode* fast = head->next; while (fast != nullptr && fast->next != nullptr ) { slow = slow->next; fast = fast->next->next; } ListNode* mid = slow->next; slow->next = nullptr ; return mid; } ListNode* merge (ListNode* l1, ListNode* l2) { ListNode dummy (0 ) ; ListNode* tail = &dummy; while (l1 != nullptr && l2 != nullptr ) { if (l1->val < l2->val) { tail->next = l1; l1 = l1->next; } else { tail->next = l2; l2 = l2->next; } tail = tail->next; } if (l1 != nullptr ) tail->next = l1; else tail->next = l2; return dummy.next; } };
分析:
归并排序。
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 class Solution {public : ListNode* mergeKLists (vector<ListNode*>& lists) { int k = lists.size (); if (k == 0 ) return nullptr ; if (k == 1 ) return lists[0 ]; int mid = (k + 1 ) / 2 ; ListNode* left = sortList (lists, 0 , mid - 1 ); ListNode* right = sortList (lists, mid, k - 1 ); return merge (left, right); } private : ListNode* sortList (vector<ListNode*>& lists, int l, int r) { if (l == r) return lists[l]; int mid = (l + r) / 2 ; ListNode* left = sortList (lists, l, mid); ListNode* right = sortList (lists, mid + 1 , r); return merge (left, right); } ListNode* merge (ListNode* l1, ListNode* l2) { ListNode dummy{0 }; ListNode* tail = &dummy; while (l1 != nullptr && l2 != nullptr ) { if (l1->val < l2->val) { tail->next = l1; l1 = l1->next; } else { tail->next = l2; l2 = l2->next; } tail = tail->next; } if (l1 != nullptr ) tail->next = l1; else tail->next = l2; return dummy.next; } };
分析:
idea from here 。取书,放书的比喻很形象。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Node {public : int key; int value; Node* pre; Node* nxt; Node (int k = 0 , int v = 0 ) : key (k), value (v) {} }; class LRUCache {private : int cap; Node* dummy; unordered_map<int , Node*> key_to_node; void remove (Node* x) void push_front (Node* x) Node* get_node (int key) ; public : LRUCache (int capacity) : cap (capacity), dummy (new Node ()) {} int get (int key) void put (int key, int value) };
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 class Node {public : int key; int value; Node* pre; Node* nxt; Node (int k = 0 , int v = 0 ) : key (k), value (v) {} }; class LRUCache {private : int cap; Node* dummy; unordered_map<int , Node*> key_to_node; void remove (Node* x) { x->pre->nxt = x->nxt; x->nxt->pre = x->pre; } void push_front (Node* x) { x->pre = dummy; x->nxt = dummy->nxt; x->pre->nxt = x; x->nxt->pre = x; } Node* get_node (int key) { auto it = key_to_node.find (key); if (it == key_to_node.end ()) return nullptr ; Node* node = it->second; remove (node); push_front (node); return node; } public : LRUCache (int capacity) : cap (capacity), dummy (new Node ()) { dummy->pre = dummy; dummy->nxt = dummy; } int get (int key) Node* node = get_node (key); return node ? node->value : -1 ; } void put (int key, int value) Node* node = get_node (key); if (node) node->value = value; else { key_to_node[key] = node = new Node (key, value); push_front (node); if (key_to_node.size () > cap) { Node* back_node = dummy->pre; key_to_node.erase (back_node->key); remove (back_node); delete back_node; } } } };
二叉树 分析:
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { TreeNode* head; public : void flatten (TreeNode* root) if (root == nullptr ) return ; flatten (root->right); flatten (root->left); root->left = nullptr ; root->right = head; head = root; } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution {public : void flatten (TreeNode* root) auto dfs = [](this auto && self, TreeNode* p) -> TreeNode* { if (p == nullptr ) return nullptr ; TreeNode* left_tail = self (p->left); TreeNode* right_tail = self (p->right); if (left_tail) { left_tail->right = p->right; p->right = p->left; p->left = nullptr ; } return right_tail ? right_tail : left_tail ? left_tail : p; }; dfs (root); } };
分析:
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution {public : TreeNode* buildTree (vector<int >& preorder, vector<int >& inorder) { if (preorder.empty ()) return nullptr ; int left_size = ranges::find (inorder, preorder[0 ]) - inorder.begin (); vector<int > pre1 (preorder.begin() + 1 , preorder.begin() + left_size + 1 ) ; vector<int > pre2 (preorder.begin() + left_size + 1 , preorder.end()) ; vector<int > in1 (inorder.begin(), inorder.begin() + left_size) ; vector<int > in2 (inorder.begin() + left_size + 1 , inorder.end()) ; TreeNode* left = buildTree (pre1, in1); TreeNode* right = buildTree (pre2, in2); return new TreeNode (preorder[0 ], left, right); } };
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : TreeNode* buildTree (vector<int >& preorder, vector<int >& inorder) { int n = preorder.size (); unordered_map<int , int > mp; for (int i = 0 ; i < n; ++i) mp[inorder[i]] = i; auto dfs = [&](this auto && dfs, int pre_l, int pre_r, int in_l, int in_r) -> TreeNode* { if (pre_l == pre_r) return nullptr ; int left_size = mp[preorder[pre_l]] - in_l; TreeNode* left = dfs (pre_l + 1 , pre_l + 1 + left_size, in_l, in_l + left_size); TreeNode* right = dfs (pre_l + 1 + left_size, pre_r, in_l + left_size + 1 , in_r); return new TreeNode (preorder[pre_l], left, right); }; return dfs (0 , n, 0 , n); } };
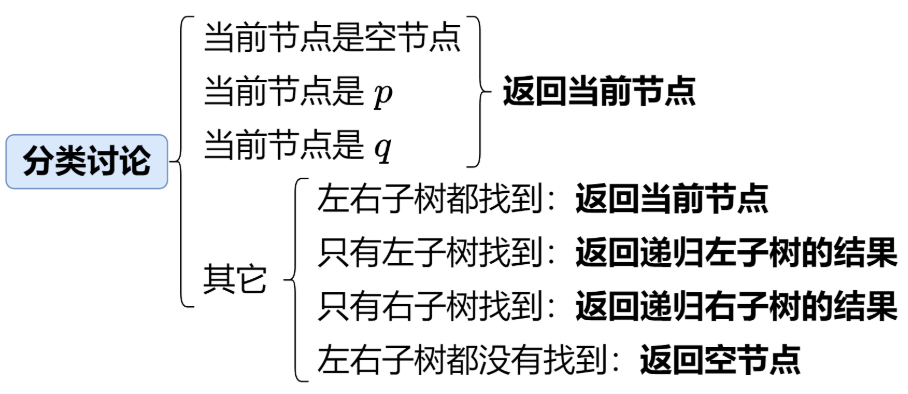
分析:
虽然可以记录根节点到这两个节点的路径,然后对比,但是有更简单的方法。图片来源
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution {public : TreeNode* lowestCommonAncestor (TreeNode* root, TreeNode* p, TreeNode* q) { if (root == nullptr || root == p || root == q) return root; TreeNode* left = lowestCommonAncestor (root->left, p, q); TreeNode* right = lowestCommonAncestor (root->right, p, q); if (left && right) return root; return left ? left : right; } };
回溯 分析:
方法1:字符串哈希
自己的写法,看到回文串就想到哈希了,笨比方法,比较麻烦。
思路是通过字符串哈希求出所有回文子串,根据每个回文子串的首地址l,把他们放到对应的vector中,之后对这个vector做dfs。
方法2:dp
把上面的vector看成一个dp数组,dp[i][j]表示s[i...j]是否是回文串,那么dp[i][j] = dp[i+1][j-1] && (s[i]==s[j]) (i<j) , dp[i][j] = 1 (i >= j)。有了这个dp数组,就可以dfs了。
方法3:记忆化搜索
上面提到的dp数组的求解过程除了可以线性递推,也可以用记忆化搜索。
AC代码:
方法1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 class Solution {public : const long long mod = 1e9 + 7 ; vector<vector<string>> partition (string s) { int len = s.size (); vector<long long > hash1 (len + 5 , 0 ) , hash2 (len + 5 , 0 ) ; vector<long long > bas (20 , 0 ) ; vector<vector<string>> vt (len + 5 , vector <string>()); vector<vector<string>> ans; s = '$' + s; for (int i = 1 ; i <= len; ++i) { hash1[i] = (hash1[i - 1 ] * 26 % mod + s[i] - 'a' + 1 ) % mod;; hash2[len - i + 1 ] = (hash2[len - i + 2 ] * 26 % mod + s[len - i + 1 ] - 'a' + 1 ) % mod; } bas[1 ] = 26 ; for (int i = 2 ; i <= 16 ; ++i) bas[i] = (bas[i - 1 ] * 26 ) % mod; int slen; long long hashz, hashf; for (int i = 1 ; i <= len; ++i) { string tmp = "" ; tmp += s[i]; vt[i].push_back (tmp); for (int j = i + 1 ; j <= len; ++j) { slen = j - i + 1 ; tmp += s[j]; hashz = (hash1[i + slen / 2 - 1 ] - hash1[i - 1 ] * bas[slen / 2 ] % mod + mod) % mod; hashf = (hash2[j - slen / 2 + 1 ] - hash2[j + 1 ] * bas[slen / 2 ] % mod + mod) % mod; if (hashz == hashf) vt[i].push_back (tmp); } } vector<string> res; auto dfs = [&](this auto && self, int u) -> void { if (u == len + 1 ) ans.push_back (res); for (int i = 0 ; i < vt[u].size (); ++i) { res.push_back (vt[u][i]); self (u + vt[u][i].size ()); res.pop_back (); } }; for (int i = 0 ; i < vt[1 ].size (); ++i) { res.push_back (vt[1 ][i]); dfs (1 + vt[1 ][i].size ()); res.pop_back (); } return ans; } };
方法2:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution {public : vector<vector<string>> partition (string s) { int n = s.size (); vector<vector<bool >> dp (n, vector <bool >(n, true )); vector<vector<string>> ans; vector<string> tmp; for (int i = n - 1 ; i >= 0 ; --i) { for (int j = i + 1 ; j < n; ++j) { dp[i][j] = (s[i] == s[j]) && dp[i + 1 ][j - 1 ]; } } auto dfs = [&](this auto && self, int l) -> void { if (l == n) { ans.push_back (tmp); return ; } for (int r = l; r < n; ++r) { if (dp[l][r]) { tmp.push_back (s.substr (l, r - l + 1 )); self (r + 1 ); tmp.pop_back (); } } }; dfs (0 ); return ans; } };
方法3:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution {public : vector<vector<string>> partition (string s) { int n = s.size (); vector<vector<int >> dp (n, vector <int >(n, 0 )); vector<vector<string>> ans; vector<string> tmp; auto judge = [&](this auto && self, int i, int j) -> int { if (dp[i][j]) return dp[i][j]; if (i >= j) return dp[i][j] = 1 ; return dp[i][j] = (s[i] == s[j] ? self (i + 1 , j - 1 ) : -1 ); }; auto dfs = [&](this auto && self, int l) -> void { if (l == n) { ans.push_back (tmp); return ; } for (int r = l; r < n; ++r) { if (judge (l, r) == 1 ) { tmp.push_back (s.substr (l, r - l + 1 )); self (r + 1 ); tmp.pop_back (); } } }; dfs (0 ); return ans; } };