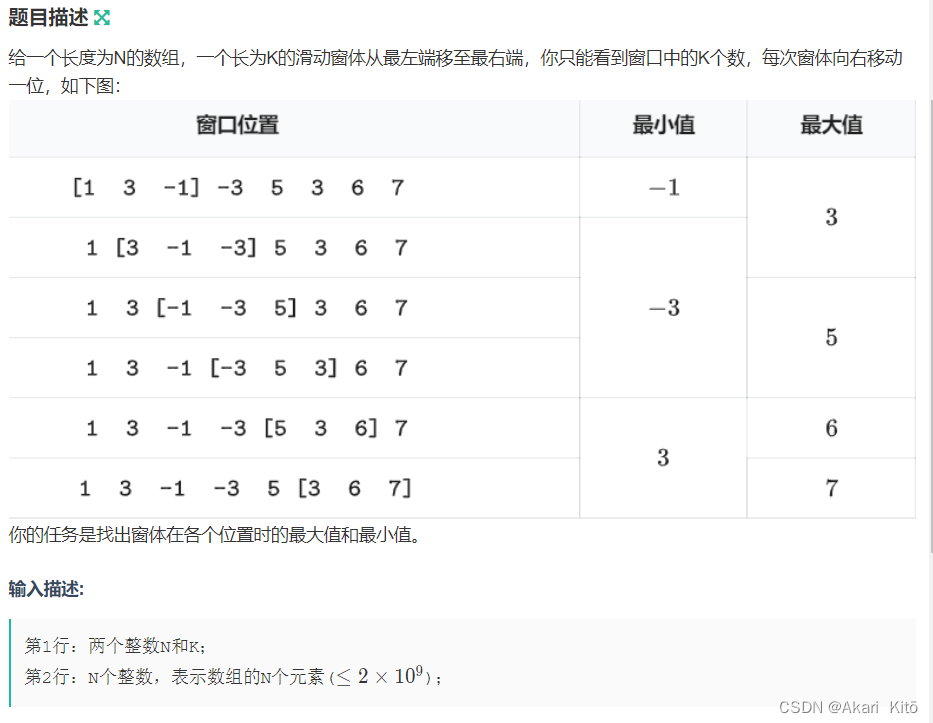
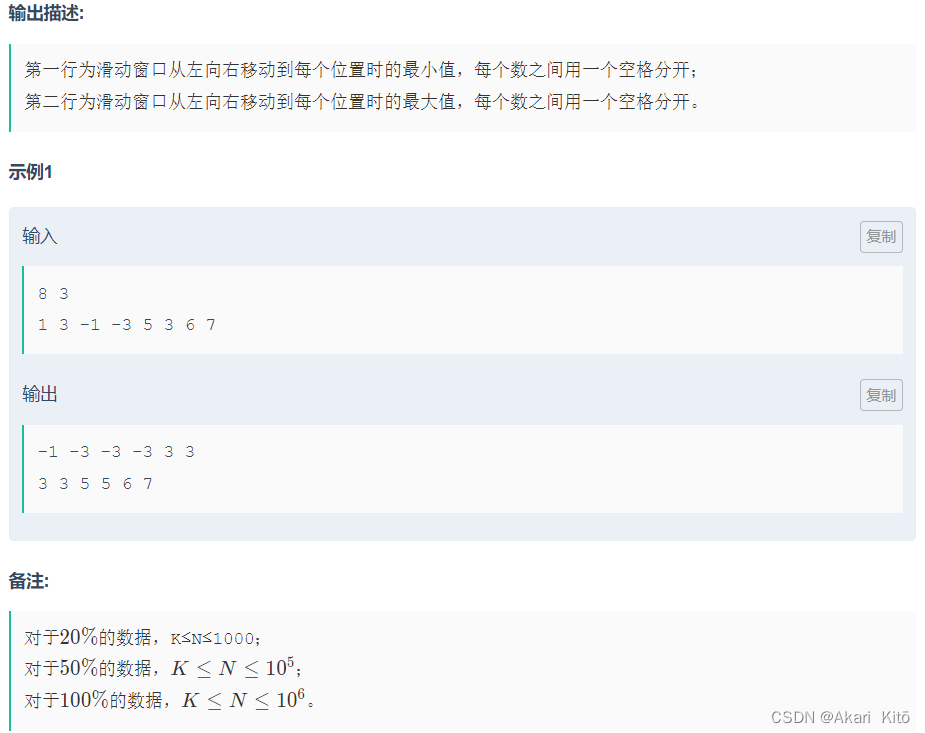
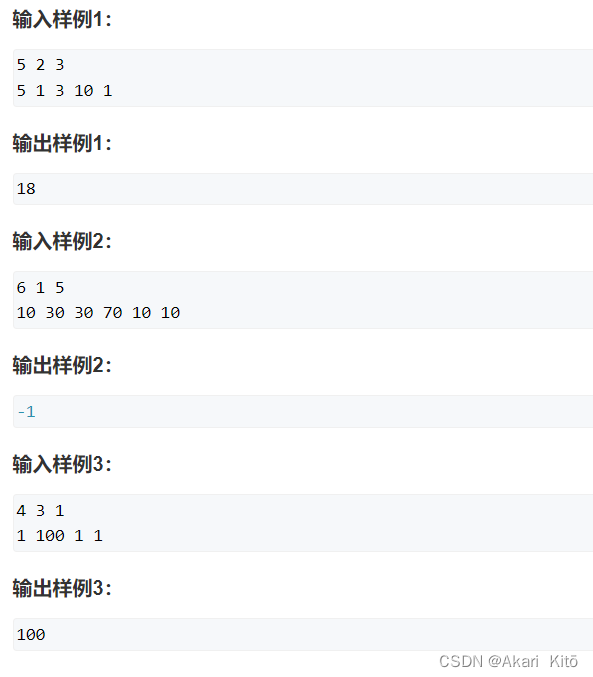
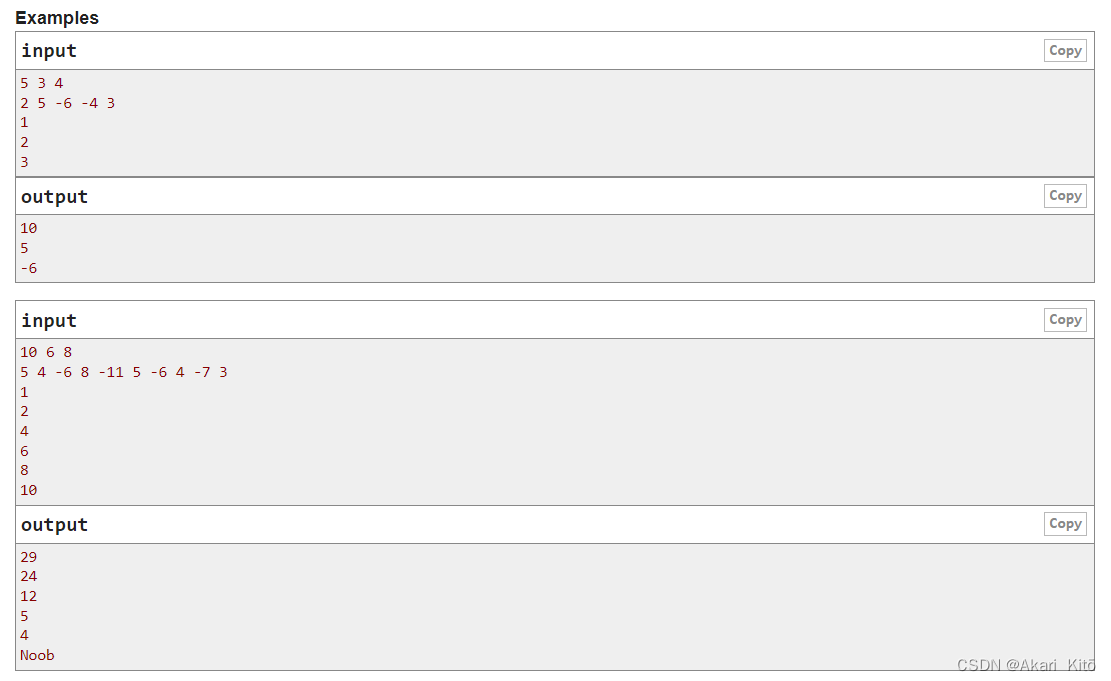
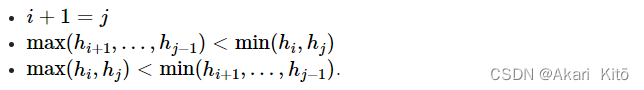单调队列/单调栈优化DP

发表于 更新于 分类于

单调队列/单调栈优化DP

滑动窗口、单调队列、单调栈、DP优化

从这几篇博客学习的：
DP优化小技巧（单调队列/单调栈）
(单调队列优化DP) 代码源每日一题 Div1 选元素（数据加强版）
算法学习笔记(67): 单调栈
牛客多校第九场I (单调栈优化dp/单调栈的常用套路)

一. 单调队列

NC50528 滑动窗口

在这里插入图片描述
img

主要思想：
  假设我们需要维护长度为$k$的区间最大值，遍历过程中，对于一个数字$a_{i+1}$，如果$a_{i+1} >= a_i$，那么我们完全可以把$a_i$的影响忽略掉。因为后面的数字比你并且生命周期还比你大，所以最大值永远不可能取到$a_i$。具体在队列中的做法就是不断访问队尾元素，小于等于当前值就出队，结束后将当前元素入队。这样的话就可以保证队首元素一定是长度为$k$的区间的最大值。（当然你需要判断队首元素与当前位置距离与$k$的大小关系确定队首元素是否需要出队）。这个过程可以用deque很容易实现，数组模拟也很容易。
AC代码：
deque：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>

using namespace std;

int n, k;
int ar[1000050];
deque<int> q;

int main()
{
    scanf("%d%d", &n, &k);

    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

    for(int i = 1; i <= n; ++i)
    {
        while(!q.empty() && q.front() + k <= i) q.pop_front();
        while(!q.empty() && ar[q.back()] >= ar[i]) q.pop_back();
        q.push_back(i);
        if(i >= k) printf("%d ", ar[q.front()]);
    }

    putchar('\n');

    q.clear();
    for(int i = 1; i <= n; ++i)
    {
        while(!q.empty() && q.front() + k <= i) q.pop_front();
        while(!q.empty() && ar[q.back()] <= ar[i]) q.pop_back();
        q.push_back(i);
        if(i >= k) printf("%d ", ar[q.front()]);
    }

    return 0;
}

数组模拟：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>

using namespace std;

int n, k;
int ar[1000050];
int p[1000050];
int l, r;//左闭右开

int main()
{
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);
    l = 0;
    r = 1;
    p[0] = 1;
    if(k == 1) printf("%d ", ar[1]);
    for(int i = 2; i <= n; ++i)
    {
        if(i - p[l] >= k && (l < r))    l++;

        while(r > l && ar[p[r - 1]] >= ar[i]) r--;
        p[r++] = i;

        if(i >= k)  printf("%d ", ar[p[l]]);
    }
    putchar('\n');
    l = 0;
    r = 1;
    p[0] = 1;
    if(k == 1)  printf("%d ", ar[1]);
    for(int i = 2; i <= n; ++i)
    {
        if(i - p[l] >= k && (l < r))    l++;

        while(r > l && ar[p[r - 1]] <= ar[i])    r--;
        p[r++] = i;

        if(i >= k)  printf("%d ", ar[p[l]]);
    }
    putchar('\n');
    return 0;
}

二. 单调队列优化dp

  当我们为了实现给动态规划的复杂度降维的时候，通常就需要单调栈/队列，通常用来维护前面状态下可以取到的最大值或者最小值，然后直接进行转移。（ygg）
img

1.daimayuan #875. 选元素（数据加强版）

  首先，我们可以看数据没加强版

AcWing 4418. 选元素

img
img
题意：
  就是对与每个长度为为$k$的子区间，至少要有一个数被选择，一共可以选择$x$个数字，目标是让选择的$x$个数字最大。
分析：
  考虑dp，定义dp[i][j]表示选了ar[i]的情况下，前$i$个数字一共有$j$个被选的情况下的最大值。
  状态转移方程：$dp[i][j] =max(dp[i][j],dp[i-k,i-1][j-1]+ar[i])$。复杂度$O(n^3)$。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll

int n, k, x;
int ar[205];
int dp[205][205];
int ans;

signed main()
{
    scanf("%lld%lld%lld", &n, &k, &x);

    for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]);
    memset(dp, 128, sizeof(dp));
    //cout << dp[0][0] << '\n';
    dp[0][0] = 0;

    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= x; ++j)
        {
            for(int p = max(0ll, i - k); p < i; ++p)
            {
                dp[i][j] = max(dp[i][j], dp[p][j - 1] + ar[i]);
            }
            //cout << i << ' ' << j << ' ' << dp[i][j] << '\n';
        }
    }

    ans = -1;
    for(int i = n - k + 1; i <= n; ++i) ans = max(ans, dp[i][x]);
    printf("%lld\n", ans);

    return 0;
}

数据加强版

  对于数据加强版，$n,k,x$的取值达到2500，$O(n^3)$一定超时。我们考虑优化，对于原来的状态转移式。$dp[i][j] =max(dp[i][j],dp[i-k,i-1][j-1]+ar[i])$，考虑以极快的速度求出$max(dp[i-k,i-1][j-1])$。本质上一个窗口大小为$k$的滑动窗口，故利用单调队列优化即可。复杂度$O(n^2)$。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

int n, k, x, top;
ll ar[2550];
ll dp[2550][2550];
ll ans;

int main()
{
    scanf("%d%d%d", &n, &k, &x);

    for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]);
    memset(dp, 128, sizeof(dp));
    //cout << dp[0][0] << '\n';
    dp[0][0] = 0;

    for(int j = 1; j <= x; ++j)
    {
        deque<int> q;
        q.push_back(0);
        for(int i = 1; i <= n; ++i)
        {
            while(!q.empty() && q.front() < i - k) q.pop_front();
            dp[i][j] = dp[q.front()][j - 1] + ar[i];
            while(!q.empty() && dp[q.back()][j - 1] <= dp[i][j - 1]) q.pop_back();
            q.push_back(i);
        }
    }

    ans = -1;
    for(int i = n - k + 1; i <= n; ++i) ans = max(ans, dp[i][x]);
    printf("%lld\n", ans);

    return 0;
}

2. C. Jump and Treasure（Gym - 103743C）2022江苏省赛

img
img
题意：
  输入$n，q，p$,之后一行$n$个数字，之后$q$行，$q$次询问。
  你现在在玩一个游戏，初始在0点，你只可以向右走，游戏有很多关，对于第$x$关，你只能走到$i$的倍数的点上，并且每步跨越的最大距离是$p$,每个点上有数字，当你到达这个点是，你的数值就会加上该点的权值，初始时你的数值为0，通关条件是到达点$n+1$及其之后的点，并且$n+1$及其之后的点的数值都为0，走到$n+1$之后的点不需要考虑他们是否是$x$的倍数，只需要考虑最大跨越距离的限制。你可以在不违规的前提下走任意多步，$q$次询问，问你对于第$x$关，通关时的最大数值。
分析：
  考虑dp，定义dp[i]表示，对于第$x$关，走到第$i$个能到达的点时所能获得的最大价值。
  转移方程：$dp[i] = max(dp[i], dp[i-p/x,i-1]+ar[i])$ (不考虑Noob的情况)。
  如果暴力跑，复杂度为$O(TLE)$,依旧考虑单调队列优化取$max$的部分。复杂度$O(nlogn)$。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const  ll inf = 0x3f3f3f3f3f3f3f3f;
int n, p, q, x;
ll ans[1000050];
int ar[1000050];
ll dp[1000050];
vector<int> vt[1000005];
int qq[1000050];
int l, r;

int main()
{
    io;
    cin >> n >> q >> p;
    for(int i = 1; i <= n; ++i) cin >> ar[i];

    for(int i = 1; i <= n; ++i)
    {
        ans[i] = -inf;
        for(int j = 0; j <= n; j += i) vt[i].push_back(j);
        vt[i].push_back(n + 1);
    }

    while(q--)
    {
        cin >> x;
        if(ans[x] != -inf) cout << ans[x] << '\n';
        else if(x > p) cout << "Noob\n";
        else
        {
            dp[0] = 0;
            l = r = 1;
            qq[r] = 0;

            for(int i = 1; i < vt[x].size(); ++i)
            {
                while(l <= r && vt[x][i] - qq[l] > p) ++l;
                dp[vt[x][i]] = dp[qq[l]] + ar[vt[x][i]];

                while(l <= r && dp[qq[r]] <= dp[vt[x][i]]) --r;
                qq[++r] = vt[x][i];

            }

            ans[x] = dp[n + 1];
            cout << ans[x] << '\n';

        }
    }

    return 0;
}

3.P1725 琪露诺（单调队列）

img
题意：
  很类似上一个题，只不过跳的方式有所不同，是给定一个$l,r$,对于当前点$i$，可以跳到$[i+l,i+r]$
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
int n, l, r;
int ar[600050];
int dp[600050];
deque<int> q;

int main()
{
    scanf("%d%d%d", &n, &l, &r);

    for(int i = 0; i <= n; ++i)
    {
        scanf("%d", &ar[i]);
        dp[i] = -inf;
    }

    dp[0] = ar[0];
    q.push_back(0);
    dp[l] = ar[l];

	//3*n是我乱写的，反正不会超时，后面那一坨的dp值都是相同的。
    for(int i = l + 1; i <= 3 * n; ++i)
    {
        while(!q.empty() && q.front() + r < i) q.pop_front();
        while(!q.empty() && dp[q.back()] <= dp[i - l]) q.pop_back();
        q.push_back(i - l);

        dp[i] = dp[q.front()] + ar[i];
        //cout << i << ' ' << dp[i] << '\n';
    }

    printf("%d\n", dp[3 * n]);

    return 0;
}

4.AcWing 135 最大子序和

img
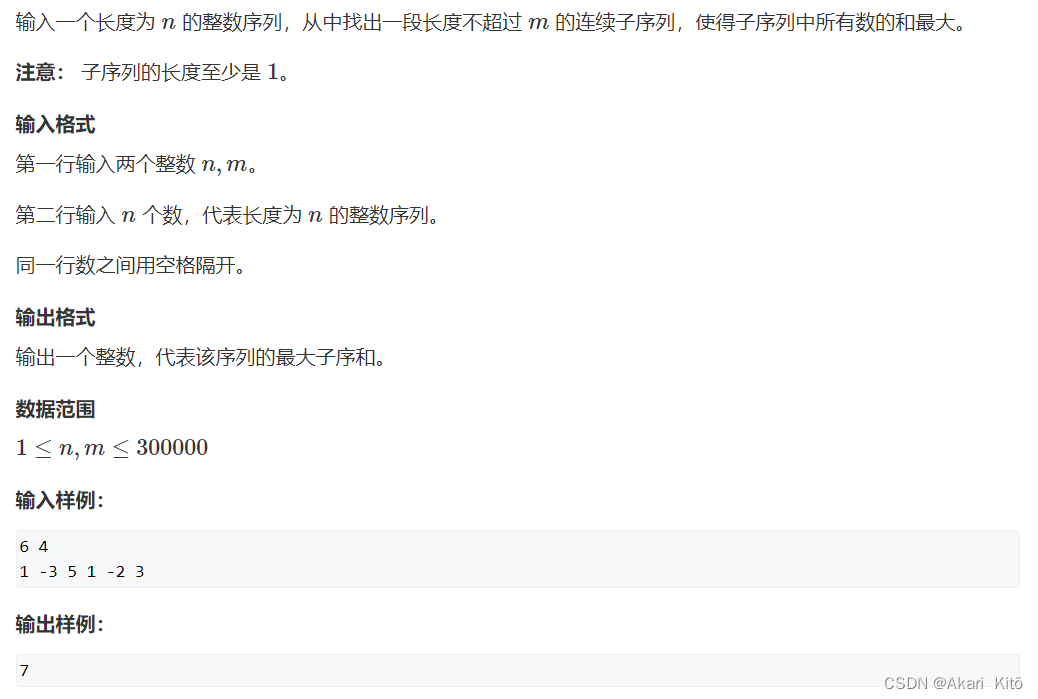
分析：
  dp[i]表示以i为结尾的一段长度不超过m的连续子序列的和的最大。
  $dp[i] = \max_{j=i-m}^{j=i-1} sum[i]-sum[j]$
  单调队列维护长度为m的区间中-sum[j]的最大值(或者sum[j]的最小值)即可$O(1)$转移，总体复杂度$O(n)$。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 3e5 + 5;
const int inf = 0x3f3f3f3f;
int n, m;
int ar[maxn];
int sum[maxn];
int dp[maxn];
deque<pair<int,int>> q;
bool flag;

void print()
{
    int ans = -inf;
    for(int i = 1; i <= n; ++i) ans = max(ans, ar[i]);
    cout << ans << '\n';
}

signed main()
{
    //io;
    cin >> n >> m;
    flag = false;
    for(int i = 1; i <= n; ++i)
    {
        cin >> ar[i];
        sum[i] = sum[i - 1] + ar[i];
        if(ar[i] > 0) flag = true;
    }

    if(!flag) print();
    else
    {
        deque<int> q;
        q.push_back(0);
        for(int i = 1; i <= n; ++i)
        {
            while(!q.empty() && i - q.front() > m) q.pop_front();
            dp[i] = sum[i] - sum[q.front()];
            while(!q.empty() && -sum[i] >= -sum[q.back()]) q.pop_back();
            q.push_back(i);
            //cout << i << ' ' << dp[i] << '\n';
        }

        int mx = -inf;
        for(int i = 1; i <= n; ++i) mx = max(mx, dp[i]);
        cout << mx << '\n';
    }


    return 0;
}

5.AcWing 1087 修剪草坪

img
img
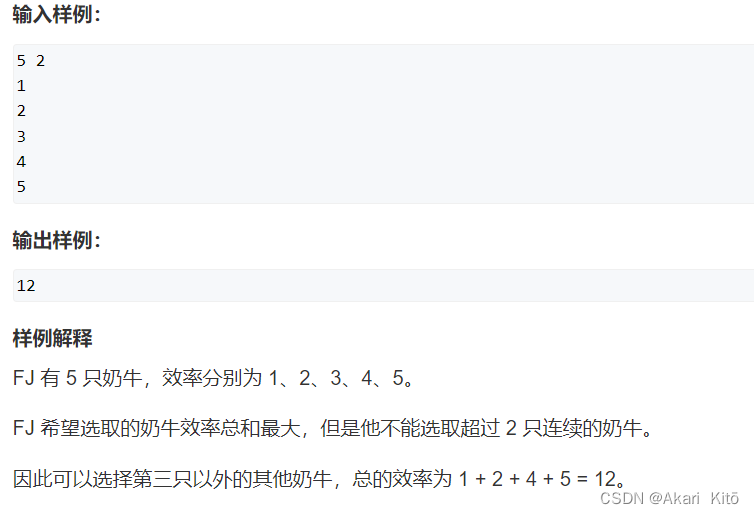
分析：
  dp[i]表示前i头牛选第i头牛的最大效率
  $dp[i] = \max_{j = i-k}^{j = i-1} dp[j - 1] + sum[i] - sum[j]$
  单调队列维护dp[j-1]-sum[j]的最大值即可。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 3e5 + 5;
const int inf = 0x3f3f3f3f;
int n, k;
int ar[maxn];
int sum[maxn];
int dp[maxn];
int gg[maxn];

signed main()
{
    io;
    cin >> n >> k;
    for(int i = 1; i <= n; ++i)
    {
        cin >> ar[i];
        sum[i] = sum[i - 1] + ar[i];
    }

    deque<int> q;
    q.push_back(0);
    gg[0] = 0;

    for(int i = 1; i <= n; ++i)
    {
        while(!q.empty() && i - q.front() > k) q.pop_front();
        dp[i] = sum[i] + gg[q.front()];
        gg[i] = -sum[i] + dp[i - 1];
        while(!q.empty() && gg[i] >= gg[q.back()]) q.pop_back();
        q.push_back(i);
        //cout << i << ' ' << dp[i] << '\n';
    }

    int mx = -inf;
    for(int i = 1; i <= n; ++i) mx = max(mx, dp[i]);
    cout << mx << '\n';


    return 0;
}

6.AcWing 1090绿色通道

img
img
分析：
  二分答案+单调队列优化dp
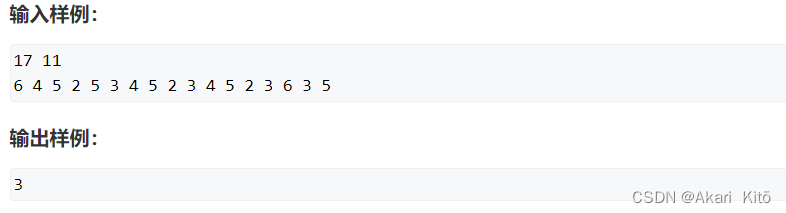
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 2e5 + 5;
const int inf = 0x3f3f3f3f;
int n, m;
int ar[maxn];
int dp[maxn];

bool judge(int k)
{
    deque<int> q;
    q.push_back(0);
    dp[0] = 0;
    for(int i = 1; i <= n; ++i)
    {
        while(!q.empty() && i - q.front() > k) q.pop_front();
        dp[i] = dp[q.front()] + ar[i];
        while(!q.empty() && dp[i] <= dp[q.back()]) q.pop_back();
        q.push_back(i);
    }

    int mi = inf;
    for(int i = n; i > n - k; --i) mi = min(mi, dp[i]);
    return mi <= m;
}

signed main()
{
    io;
    cin >> n >> m;
    for(int i = 1; i <= n; ++i) cin >> ar[i];

    int l = 0, r = n;
    while(l <= r)
    {
        int mid = (l + r) >> 1;
        if(judge(mid)) r = mid - 1;
        else l = mid + 1;
    }

    cout << r << '\n';

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define endl '\n'
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 5e4 + 5;
const int inf = 0x3f3f3f3f;
int n, t;
int ar[maxn];
int sum[maxn];
int gg[maxn];
int dp[maxn];

bool judge(int mid)
{
    deque<int> q;
    memset(dp, 0, sizeof(dp));
    q.push_back(0);
    gg[0] = 0;

    for(int i = 1; i <= n; ++i)
    {
        while(!q.empty() && i - q.front() > mid) q.pop_front();
        dp[i] = sum[i] + gg[q.front()];
        gg[i] = -sum[i] + dp[i - 1];
        while(!q.empty() && gg[i] >= gg[q.back()]) q.pop_back();
        q.push_back(i);
    }

    int mx = -inf;
    for(int i = 1; i <= n; ++i) mx = max(mx, dp[i]);
    if(sum[n] - mx > t) return false;
    else return true;
}

signed main()
{
    io;
    cin >> n >> t;
    for(int i = 1; i <= n; ++i)
    {
        cin >> ar[i];
        sum[i] = sum[i - 1] + ar[i];
    }

    if(sum[n] <= t) 
    {
        cout << 0 << '\n';
        return 0;
    }

    int l = 1, r = n, mid;
    while(l <= r)
    {
        mid = (l + r) >> 1;
        if(judge(mid)) r = mid - 1;
        else l = mid + 1;
    }
    cout << r + 1 << '\n';

    return 0;
}

三. 单调栈

两大用处：
1.NGE问题（Next Greater Element），也就是，对序列中每个元素，找到下一个比它大的元素。
2.两元素间所有元素均(不)大/小于这两者

1. P5788 【模板】单调栈

img
img
（其实也可以用单调队列，不需要队首元素出队的单调队列)
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>

using namespace std;

int n;
int ar[3000050];
stack<int> st;
int ans[3000050];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

    ans[n] = 0;
    st.push(n);

    for(int i = n - 1; i > 0; --i)
    {
        while(!st.empty() && ar[st.top()] <= ar[i]) st.pop();

        if(!st.empty()) ans[i] = st.top();
        else ans[i] = 0;

        st.push(i);
    }

    for(int i = 1; i <= n; ++i) printf("%d ", ans[i]);
    putchar('\n');

    return 0;
}

2.P1823 [COI2007] Patrik 音乐会的等待

img
img
（区间1~i内元素大小关系和单调栈内元素情况）
img
img
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll

int n;
int ar[500050];
stack<pair<int, int> > st;
pair<int, int> pi;
int ans, cnt;

signed main()
{
    scanf("%lld", &n);
    for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]);

    st.push({ar[1], 1});
    for(int i = 2; i <= n; ++i)
    {
        int cnt = 1;
        while(!st.empty() && st.top().first <= ar[i])
        {
            pi = st.top();
            st.pop();
            //cout << pi.first << ' ' << pi.second << '\n';
            ans += pi.second;
            if(pi.first == ar[i]) cnt = pi.second + 1;
            else cnt = 1;
        }
        if(!st.empty()) ++ans;
        st.push({ar[i], cnt});
        //cout << i << ' ' << ans << '\n';
    }

    printf("%lld\n", ans);

    return 0;
}

四. 单调栈优化dp

1.CF1313C2 Skyscrapers (hard version)

img
img
题意：
  输入一个$n$，之后输入$n$个数字$ar[i]$。
  让你选择一个点作为山峰。假设选择点$pos$作为山峰，其他的$n-1$点的高度将发生变化。假设修改后的高度记为$h[i]$,对于1~pos-1中的一个点i,必须满足$h[i]=min(h[i+1],ar[i])$，对于pos+1~n中的一个点i,必须满足$h[i] = min(h[i-1],ar[i])$。求$\sum_1^n h[i]$的最大值。输出取最大值时的h[i]数组。
分析：
  首先，我们可以看一下easy版本。区别在于n的大小。easy版本n最大1000。$O(n^2)$能过。我们考虑dp，定义dp1[i],dp2[i]分别表示选择$i$作为山峰时$i$极其左侧的最大值。答案就是$max(dp1[i]+dp2[i]-ar[i])$。
  我们考虑快速求dp1[i]的方法，假设ar[j]是$i$之前第一个满足ar[j]<=ar[i]的元素，那么$dp1[i]=dp1[j]+(i-j)\times ar[i]$。而对于第一个小于等于的元素，显然可以利用单调栈快速找出。（dp2求法同理）复杂度$O(n)$。
  （单调栈用法1，利用单调栈找到区间内第一个比他大/小的元素)
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

int n, pos;
ll ar[500050];
ll dp1[500050];
ll dp2[500050];
ll ans[500050];
ll mx;
stack<ll> st;

void work()
{
    int tmp = pos;
    ll mxx = ar[tmp];
    ans[tmp] = ar[tmp];
    while(tmp > 0)
    {
        --tmp;
        ans[tmp] = min(mxx, ar[tmp]);
        mxx = ans[tmp];
    }

    tmp = pos;
    mxx = ar[tmp];
    while(tmp < n)
    {
        ++tmp;
        ans[tmp] = min(mxx, ar[tmp]);
        mxx = ans[tmp];
    }

    for(int i = 1; i <= n; ++i) printf("%lld ", ans[i]);
    putchar('\n');
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]);

    st.push(0);
    for(int i = 1; i <= n; ++i)
    {
        while(!st.empty() && ar[st.top()] >= ar[i]) st.pop();

        dp1[i] = dp1[st.top()] + (i - st.top()) * ar[i];
        st.push(i);
    }

    while(!st.empty()) st.pop();
    st.push(n + 1);
    for(int i = n; i > 0; --i)
    {
        while(!st.empty() && ar[st.top()] >= ar[i]) st.pop();

        dp2[i] = dp2[st.top()] + (st.top() - i) * ar[i];
        st.push(i);
    }

    for(int i = 1; i <= n; ++i)
    {
        if(dp1[i] + dp2[i] - ar[i] > mx)
        {
            mx = dp1[i] + dp2[i] - ar[i];
            pos = i;
        }
    }

    work();

    return 0;
}

img
（295是正解，换成解绑之后的cin，cout用线段树暴力维护居然卡过了)。

2.CF1407D Discrete Centrifugal Jumps

img
img
题意：
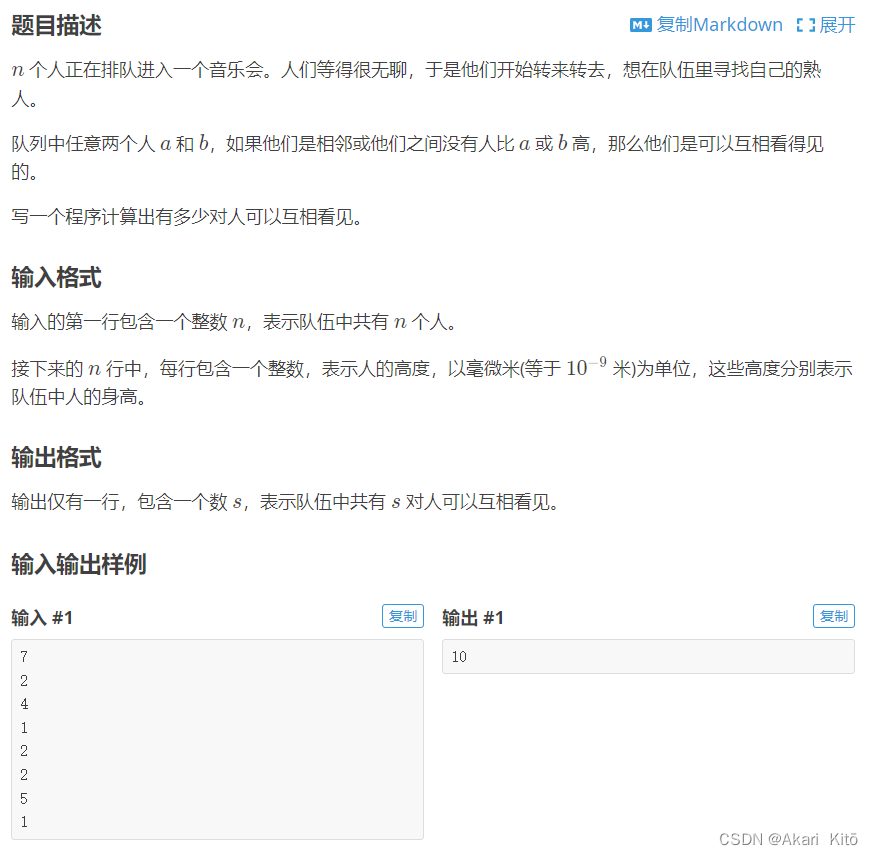
  输入一个n，之后n个数字ar[i]。
  一开始你在位置1，你要到达位置n，从位置i到位置j必须满足一下条件之一。
img
  问你到达n最少需要跳几步。
分析：
  单调栈的用法2，找两元素间所有元素均(不)大/小于这两者
img
（区间1~i内元素大小关系和单调栈内元素情况）
  借助这个图理解和P1823 [COI2007] Patrik 音乐会的等待这个题理解一下。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>

using namespace std;

int n;
stack<int> st1, st2;
int dp[300050];
int ar[300050];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

    memset(dp, 0x3f, sizeof(dp));

    dp[1] = 0;
    for(int i = 1; i <= n; ++i)
    {
        dp[i] = min(dp[i], dp[i - 1] + 1);
        while(!st1.empty() && ar[st1.top()] <= ar[i])
        {
            int pos = st1.top();
            st1.pop();
            if(!st1.empty() && ar[i] > ar[pos]) dp[i] = min(dp[st1.top()] + 1, dp[i]);
        }
        st1.push(i);

        while(!st2.empty() && ar[st2.top()] >= ar[i])
        {
            int pos = st2.top();
            st2.pop();
            if(!st2.empty() && ar[i] < ar[pos]) dp[i] = min(dp[st2.top()] + 1, dp[i]);
        }
        st2.push(i);
    }

    printf("%d\n", dp[n]);

    return 0;
}

3.牛客多校第九场I The Great Wall II

img
img
img
题意：
  输入一个n，之后输入数组ar[n]。你需要将区间[1,n]分成k个子区间，这k个区间两两不交，且并集是全集。每个子区间的值是这个区间中最大的那个数字，你需要最小化这k个区间的值的和。输出k取1~n时对应的答案。
分析：
官方题解：
img

img

img

说人话：
img

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
int n;
int ar[8005];
int dp[8005][8005];
struct node
{
    int val, mi, mi_dp;//ar[k],dp[k][j - 1],min(dp[k][j])
}st[8005];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

    memset(dp, 0x3f, sizeof(dp));

    dp[0][0] = 0;

    for(int j = 1; j <= n; ++j)
    {
        int top = 1;
        st[top] = {inf, inf, inf};
        for(int i = 1; i <= n; ++i)
        {
            int mi = dp[i - 1][j - 1];
            while(top >= 1 && st[top].val <= ar[i]) mi = min(mi, st[top--].mi);
            st[top + 1] = {ar[i], mi, min(mi + ar[i], st[top].mi_dp)};
            ++top;
            dp[i][j] = st[top].mi_dp;
        }
        printf("%d\n", dp[n][j]);
    }

    return 0;
}