Codeforces Round#829 (Div. 2)
C2. 数学/思维
D. 数学/思维
E. 数学/概率
C1. Make Nonzero Sum (easy version)
C2. Make Nonzero Sum (hard version)



题意:
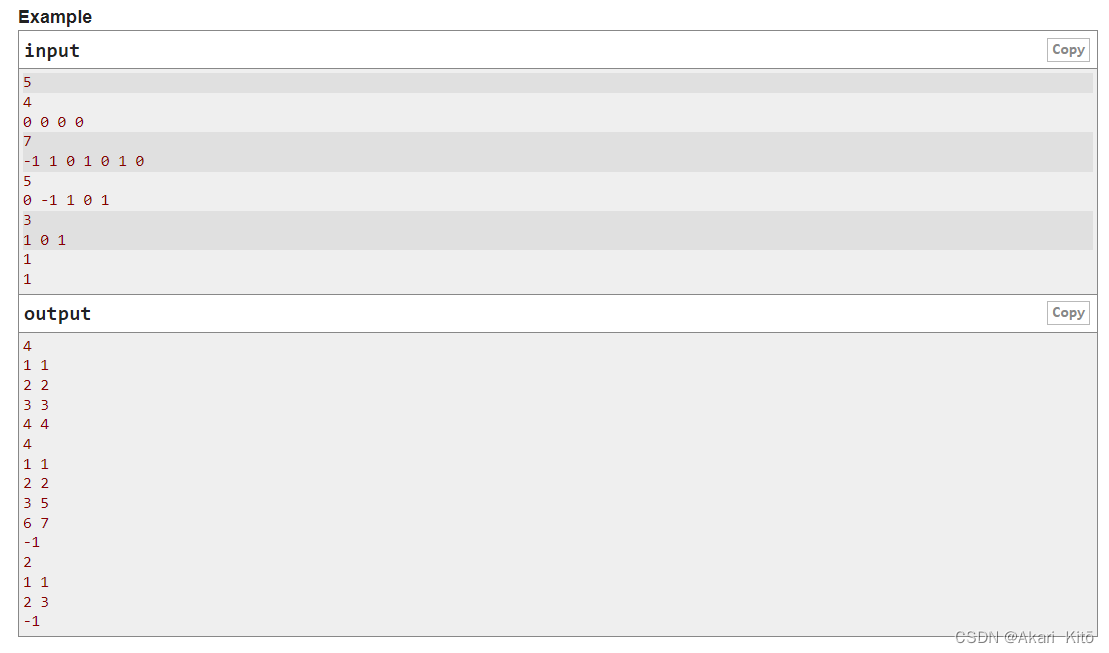
对于每个样例,输入一个n,代表数组的长度,这个数组中的元素只有-1,0,1(easy版本没有0,这是唯一的区别),你可以把这个区间[1,n]分成k个子区间$(1<=k<=n)$,这个k个子区间两两不相交,k个子区间的和是全集[1,n]。对于每个元素,如果在其子区间内是第奇数个,那么取它的原始值,如果是第偶数个,取它的相反数,这n个数字的求和。问你是否存在一种分法,使得和为0,存在输出分法(先输出分成几个子区间,之后输出每个子区间的l,r,要求按照l升序排序),不存在输出-1。
分析:
对于easy版本,统计1的个数和-1的个数,之后做差的cx,判断差值的奇偶性,如果为奇,则为-1,否则存在方案。对于相等的部分,互为相反数,都取他们原始值,正好可以抵消掉,对于多出来的那一部分,可以一半取相反数消耗,故奇数为-1,偶数正好消耗,那么我们就需要找cx/2对相邻的1或-1(数量多的那一个数字),每一对作为一个子区间,剩下的每个数字单独作为一个子区间即可。需要说明的是,一定存在cx/2对相邻的(考虑最极端的情况,1和-1交替出现都满足,故一定存在)。
对于hard版本,easy版本的解法显然不适用。
我们定义一个变量sum,用于记录前缀和。之后遍历整个数组,当$sum = 0$时,无论当前数字是-1,0还是1,都取其原始值,当$sum = 1$时,当前数字是0和-1时,取其原始值,是1时,取其相反数,并标记一下这一位(利用一个bool数组),当$sum = -1$时,当前数字是0和1时,取其原始值,是-1是,取其相反数并标记。可以发现在遍历的过程中,sum的取值只可能是-1,0,1,并且不会出现连续两个元素都需要标记的情况。遍历完后,看sum是否等于0,不等于即不存在,等于存在,方案为标记的元素和其前一个元素为一个区间,剩余元素单独一个区间即可。(这个解法同样适用于easy版本)。
AC代码:
easy版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| #include <bits/stdc++.h>
using namespace std;
int t, n;
int ar[200050];
int cnt1, cnt2;
vector<pair<int,int> > vt;
bool boo[200050];
void init()
{
vt.clear();
cnt1 = cnt2 = 0;
for(int i = 1; i <= n; ++i) boo[i] = false;
}
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%d", &n);
init();
for(int i = 1; i <= n; ++i)
{
scanf("%d", &ar[i]);
if(ar[i] == 1) ++cnt1;
else ++cnt2;
}
if(abs(cnt1 - cnt2) & 1)
{
printf("-1\n");
continue;
}
if(cnt1 > cnt2)
{
int k = (cnt1 - cnt2) / 2;
for(int i = 1; i <= n; ++i)
{
if(k == 0) break;
if(ar[i] == 1 && ar[i + 1] == 1 && !boo[i] && !boo[i + 1])
{
vt.push_back(make_pair(i, i + 1));
boo[i] = boo[i + 1] = true;
--k;
}
}
}
else
{
int k = (cnt2 - cnt1) / 2;
for(int i = 1; i <= n; ++i)
{
if(k == 0) break;
if(ar[i] == -1 && ar[i + 1] == -1 && !boo[i] && !boo[i + 1])
{
vt.push_back(make_pair(i, i + 1));
boo[i] = boo[i + 1] = true;
--k;
}
}
}
for(int i = 1; i <= n; ++i)
{
if(!boo[i]) vt.push_back(make_pair(i, i));
}
sort(vt.begin(), vt.end());
printf("%d\n", vt.size());
for(int i = 0; i < vt.size(); ++i) printf("%d %d\n", vt[i].first, vt[i].second);
}
return 0;
}
|
hard版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include <bits/stdc++.h>
using namespace std;
int t, n;
int ar[200050];
bool boo[200050];
vector<pair<int,int>> vt;
int sum, cnt;
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);
sum = cnt = 0;
for(int i = 1; i <= n; ++i) boo[i] = false;
vt.clear();
for(int i = 1; i <= n; ++i)
{
if(sum == 0) sum += ar[i];
else if(sum == 1)
{
if(ar[i] == 1)
{
boo[i] = true;
sum = 0;
++cnt;
}
else sum += ar[i];
}
else
{
if(ar[i] == -1)
{
boo[i] = true;
sum = 0;
++cnt;
}
else sum += ar[i];
}
}
if(sum != 0)
{
printf("-1\n");
continue;
}
printf("%d\n", n - cnt);
for(int i = n; i > 0; --i)
{
if(!boo[i]) vt.push_back({i, i});
else
{
vt.push_back({i - 1, i});
--i;
}
}
sort(vt.begin(), vt.end());
for(int i = 0; i < vt.size(); ++i) printf("%d %d\n", vt[i].first, vt[i].second);
}
return 0;
}
|
D. Factorial Divisibility


题意:
对于每个样例,输入n和x,之后读入一个长度为n的数组a。问你$a_i! + a_2! + …+a_n!$能否被$x!$整除。
分析:
应该是考虑$a_i! + a_2! + …+a_n!$能否表示为$k\times x!$的形式。
再根据数据范围$a_i <= x$,考虑如何将$a_i! + a_2! + …+a_n!$表示成$k \times x!$的形式。
即需要将$a_i! + a_2! + …+a_n!$中$a_i<x$的项消掉,而$(i + 1) \times i! = (i + 1)!$又由于是加法可提公因式,考虑利用这个递推式将$a_i<x$的项消掉。能消掉为Yes,否则No。
具体解法,可以定义一个cnt数组cnt[i]表示数字i在数组a中出现的次数,每i + 1个i就相当于一个i+1。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include <bits/stdc++.h>
using namespace std;
int n, x;
int ar[500050];
int cnt[500050];
bool flag;
int main()
{
scanf("%d%d", &n, &x);
for(int i = 1; i <= n; ++i)
{
scanf("%d", &ar[i]);
++cnt[ar[i]];
}
for(int i = 1; i < x; ++i)
{
if(cnt[i] % (i + 1) == 0) cnt[i + 1] += cnt[i] / (i + 1);
else
{
printf("No\n");
flag = true;
break;
}
}
if(!flag) printf("Yes\n");
return 0;
}
|
E. Wish I Knew How to Sort

题意:
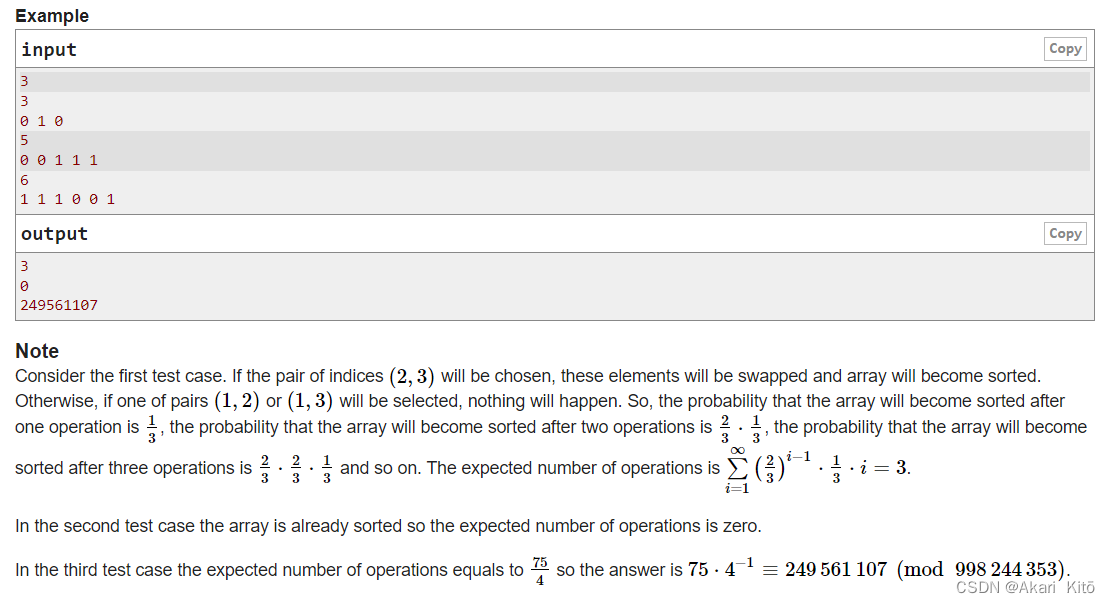
对于每个样例,输入一个n,之后一个长度为n的数组,这个数组中的数字只由0和1组成。你可以进行操作,操作是指选择一个二元组$(l,r)$满足$l <= r$,之后$swap(a_i, a_j)$,每次操作选择的二元组的概率相同。问你使原数组变成一个升序的数组的期望操作次数是多少。
分析:
假设数组中一共有k个0,而前k个元素中有c个1。那么一次成功的操作就是选择这c个1中的任意一个作为l,选择位置不在前k的一个0(一定也有c个满足这样的点)作为r,这个概率是$P = 2 \times c^2 / n(n-1)$,而成功操作1次的期望$E = 1/p$。(伯努利试验/几何分布)
而这个问题的答案就是成功操作c次的期望,对于这个期望怎么求,我们考虑掷硬币,掷出4次正面朝上的期望投掷次数可以表示为:掷出1次朝上的期望+掷出1次朝上的期望+掷出1次朝上的期望+掷出1次朝上的期望(和的期望等于期望的和),而在这个题目中同理,只不过每次成功操作的期望操作次数不同。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
ll t;
ll ar[200050];
ll n, ans;
ll k, c, tmp;
ll pow_mod(ll a, ll n)
{
ll ans = 1;
a %= mod;
while(n)
{
if(n & 1) ans = (ans * a) % mod;
a = (a * a) % mod;
n >>= 1;
}
return ans;
}
int main()
{
scanf("%lld", &t);
while(t--)
{
ans = k = c = 0;
scanf("%lld", &n);
for(int i = 1; i <= n; ++i)
{
scanf("%lld", &ar[i]);
if(ar[i] == 0) ++k;
}
for(int i = 1; i <= k; ++i) if(ar[i]) ++c;
tmp = c;
for(int i = 1; i <= c; ++i)
{
ans = (ans + (n * (n - 1) % mod * pow_mod(2ll * tmp * tmp, mod - 2)) % mod) % mod;
--tmp;
}
printf("%lld\n", ans);
}
return 0;
}
|







