AtCoder Beginner Contest 274 D E F
AtCoder Beginner Contest 274 D E F
D - Robot Arms 2 【dp】

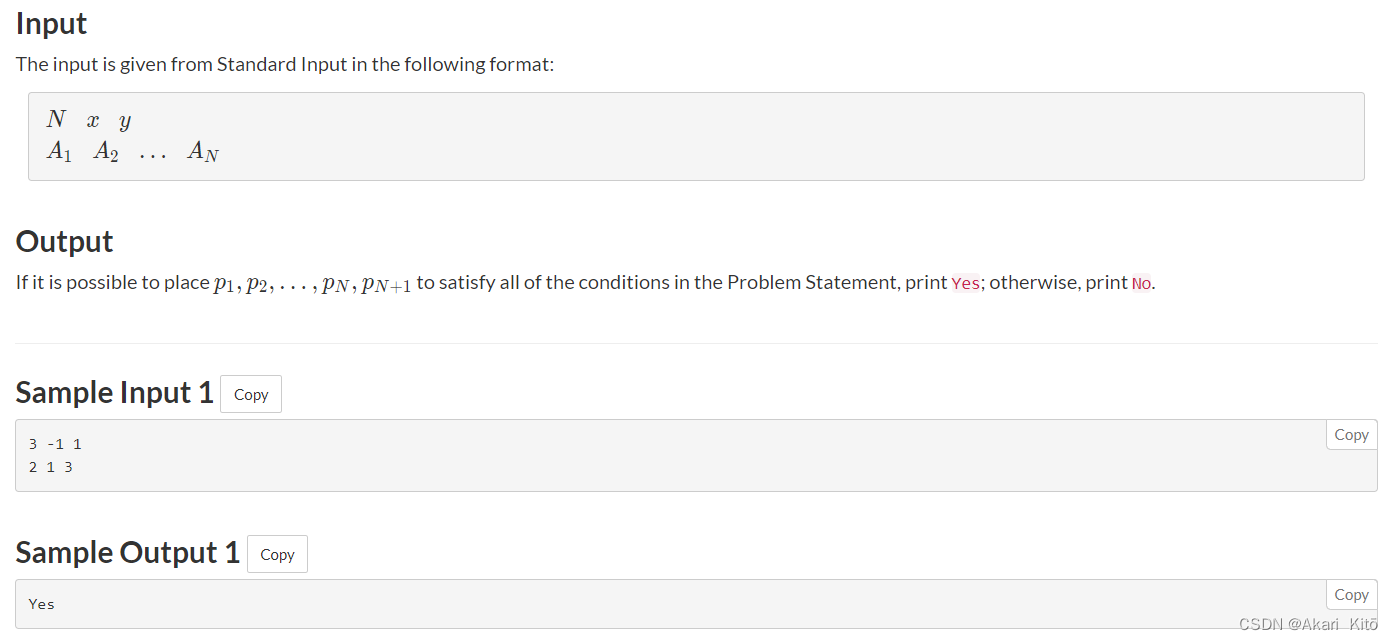
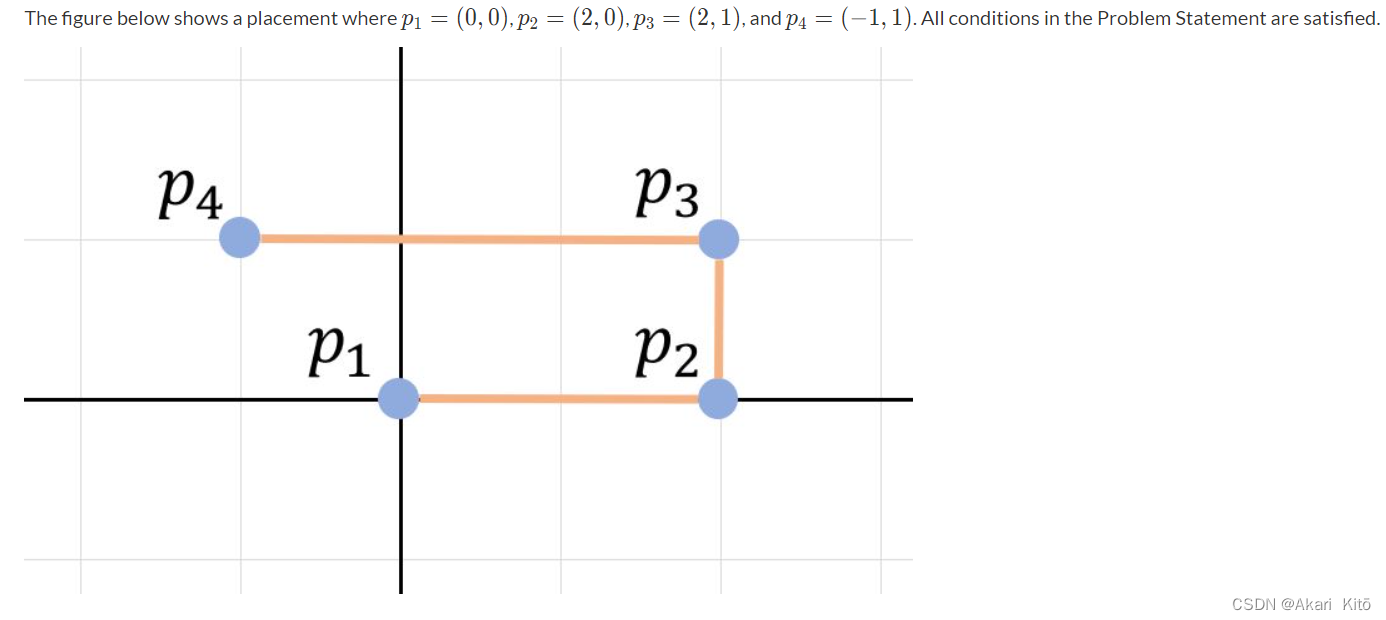
题意:
先输入,n,x,y,表示可以走n次,终点是(x,y),起点是(0,0),之后输出n个数字,第i个数字$a_i$表示第i次可以走多远,每次只能横着走或者竖着走,如果上一次是横着走,这一次必须竖着走,上一次是竖着,这一次必须横着,第一次必须由点(0,0)走到(ai,0),问你是否存在一种符合要求的走法能走到终点。
分析:
做dp,dp数组定义为bool,表示能否走到当前位置 dp[2][10005]
或者整两个STL容器转移也可以。
整体做法比较暴力。
AC代码:
1 |
|
E - Booster 【状压dp】

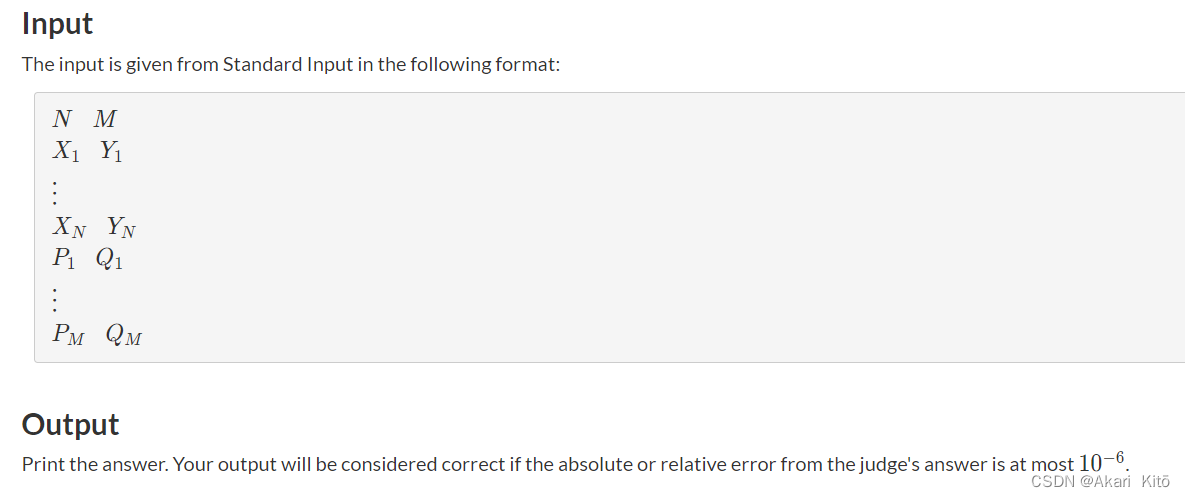
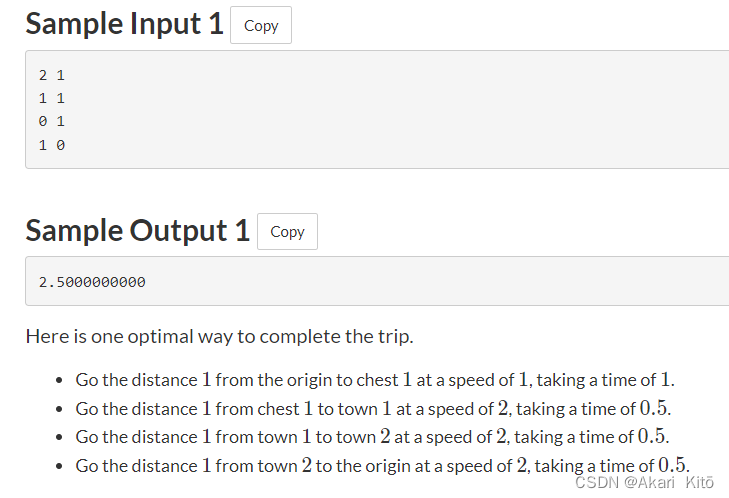
题意:
输入n,m代表有n的城市和m个宝箱,n+m行给出城市和宝箱的坐标,一开始在(0,0),你需要经过n个城市并且回到起点,起始时你的速度是1。宝箱不是必须的,但是每获取一个宝箱,你的斯必得就会翻倍。同一个地点的宝箱不可多次获取,问你最少需要多少时间回到起点。
分析:
状压dp
max(n)+max(m) = 17,$O(2^{n+m}\times(n+m)^2)$可以接受。
对于状态,需要用一个二进制下长度为n+m的数组表示,前m位表示走过的宝箱,后n位表示经过的城市,状态的转移的时候先计算一下速度,之后跟普通的状压一样,统计答案的时候,一方面,只需要统计后n位全是1的状态,另一方面,计算回到起点的时间,也是先计算速度。
AC代码
1 |
|
F - Fishing


题意:
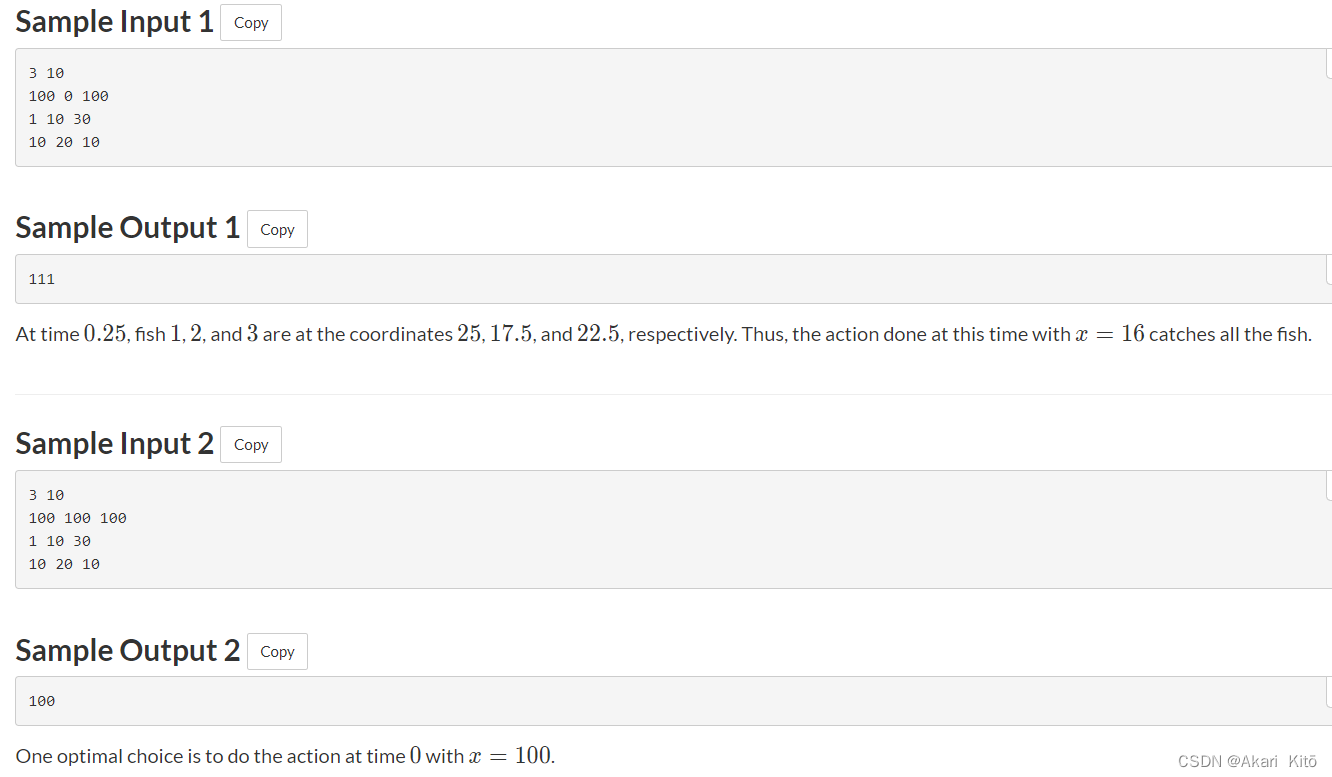
输入n和a,表示有n条鱼和一张长度为a的渔网。
之后n行每行三个数字,分别表示每条鱼的权值,起始坐标,速度,鱼会随着时间移动,问你这张长度为a的渔网最多能获得权值为多少的鱼。
分析:
枚举每一条鱼作为渔网左界的情况,可获取的权值最大值(像坐标x,时间t等变量都是double,理应排除,想到枚举n,即每一条鱼)。作为渔网的左界是为了处分利用取最大值。
之后对于剩下的n-1条鱼,随着时间流动都有三种情况,1是永远不会进入渔网中,2是进入一次渔网,出去一次渔网,之后永远不会进入(可能0时刻就进入了),3是一直在渔网内。把可能的鱼进出网时间求出,放入一个数组中(进网权值算w,出网算-w),按照时间排序,遍历一遍求前缀和即可(任何一个位置的前缀和都是合理的,因为同时处理了进网时间和出网时间,权值也做了正负区分)。
做个简单的分类讨论。(简单的高一物理追只因与相遇问题)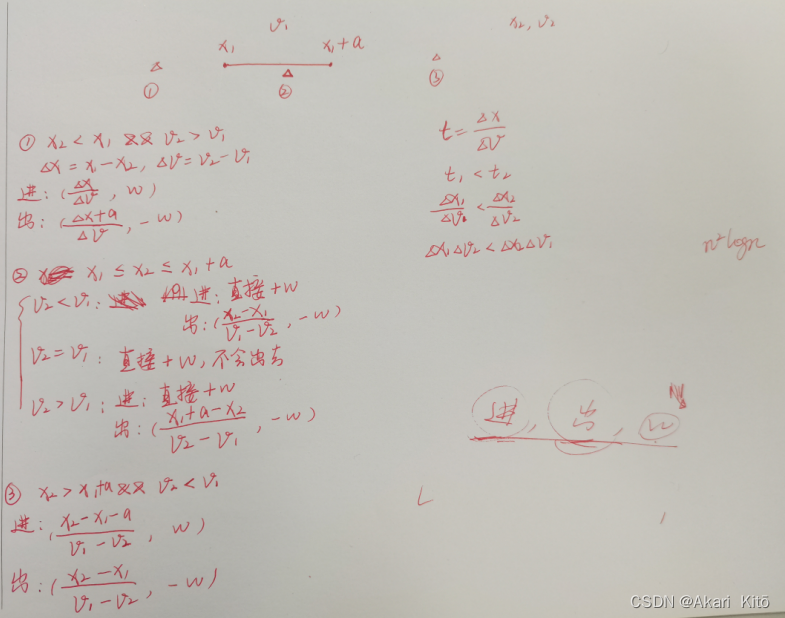
AC代码:
1 |
|