Educational Codeforces Round 138 (Rated for Div. 2)

发表于 更新于 分类于

Educational Codeforces Round 138 (Rated for Div. 2)

C. 博弈
D. 数论
E. 多源01bfs

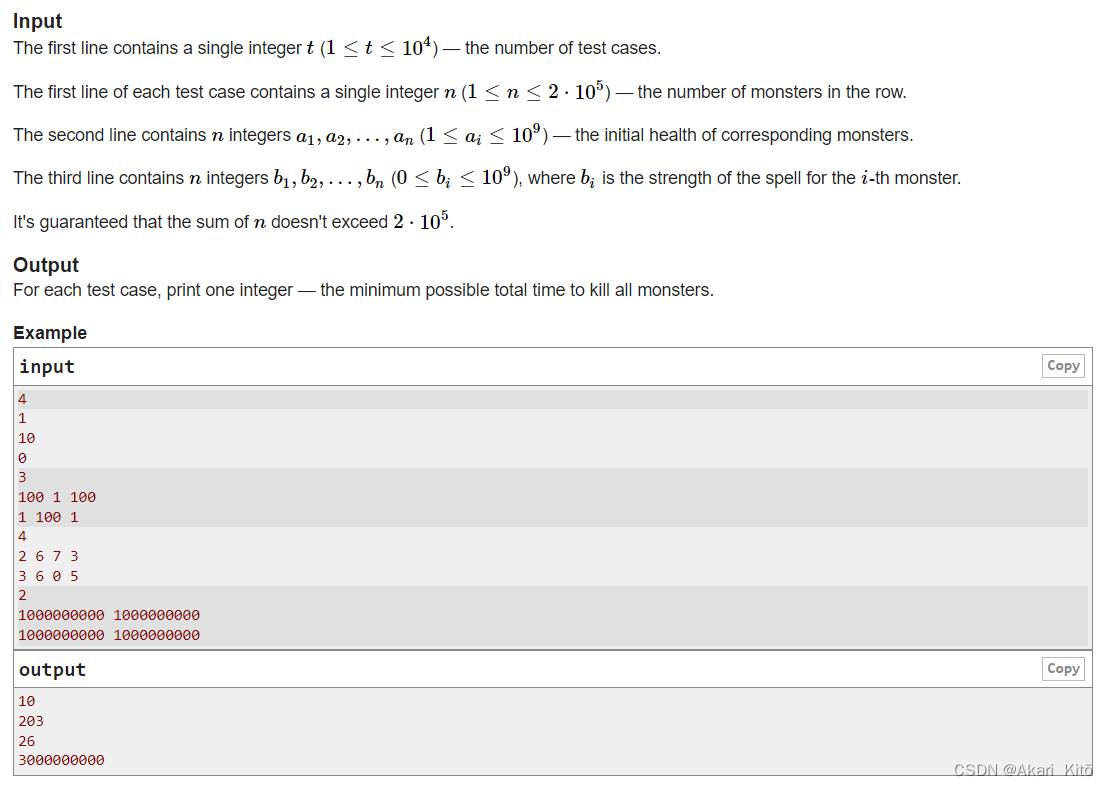
B. Death’s Blessing

img

img

img

题意：
  对于每个样例，输入一个n，表示有n个怪，每个怪有两个属性，一个叫血量a，一个叫魔法b（我瞎编的，不影响)，杀死一个血量为a的怪需要的时间为a，一个怪(ai,bi)死后，它周围的两个怪的血量会增加bi，即怪(ai-1, bi-1)->(ai-1 + bi, bi),(ai+1, bi+1)->(ai+1 + bi, bi+1),特别的，如果怪位于边界，它将之后给旁边的一个怪加血量上限，最后一个怪直接不会给任何人加。每个怪死后，右边的怪都会过来填充它的位置。
分析：
  首先，ans至少为$\sum_{1}^{n}a_i$,在此基础上考虑bi如何添加，对于每个怪，它死的时候分三种情况，死在边界上，死在中间，最后一个死，分别对答案的贡献是$b_i,2b_i,0$,只能有一个最后死，故让bi最大的那个最后死，其它都死在边界上。
*AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

const ll inf = 0x3f3f3f3f3f3f3f3f;
int t, n;
ll ar[200050];
ll br[200050];
ll ans, sum, mx;

int main()
{
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        ans = 0;
        sum = 0;
        mx = 0;
        for(int i = 1; i <= n; ++i)
        {
            scanf("%lld", &ar[i]);
            ans += ar[i];
        }

        for(int i = 1; i <= n; ++i)
        {
            scanf("%lld", &br[i]);
            sum += br[i];
            mx = max(mx, br[i]);
        }

        ans += sum - mx;
        printf("%lld\n", ans);

    }
    return 0;
}

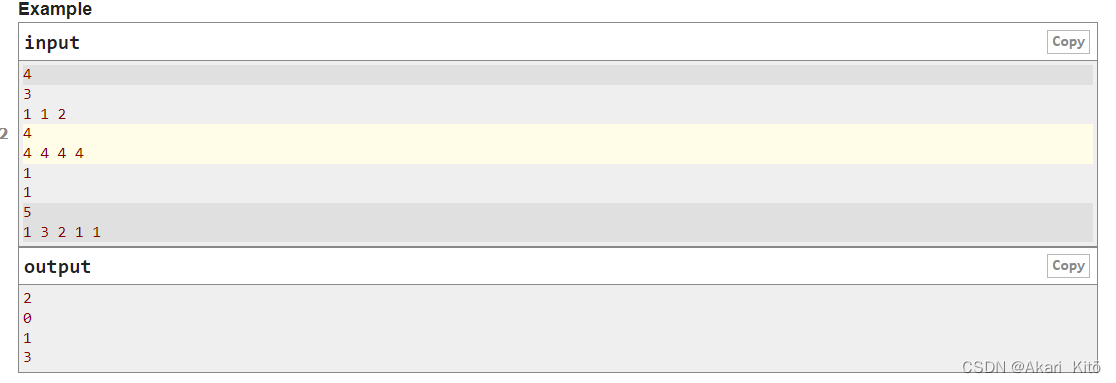
C. Number Game

img

img

题意：
  经典爱丽丝&鲍勃
  对于每个样例，输入一个n，之后输入一个长度为n的数组。
  进行进行k轮博弈，对于第$i$轮，爱丽丝需要删除一个小于等于$k-i+1$的数字，鲍勃需要将剩下的数字中任意一个数字加上$k-i+1$每一轮都是爱丽丝先手。如果有一轮谁无法操作了，谁就输了，k轮能够成功结束的话也是爱丽丝赢。两个人都聪明秃顶，都想让自己赢对方输，求爱丽丝能赢的最大的k。
分析：
  爱丽丝每次删除小于等于$k-i+1$的数字中最大的哪个，鲍勃每次对剩下数字中最小的那个数字加上$k-i+1$，由于数据范围很小完全可以暴力。$O(n^2logn t)$
*AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>

using namespace std;

int t, n;
int ar[105];
int br[105];
const int inf = 0x3f3f3f3f;

bool judge(int x)
{
    int pos;
    for(int i = 1; i <= x; ++i)
    {
        sort(ar + 1, ar + n + 1);
        pos = lower_bound(ar + 1, ar + n + 1, x - i + 1) - ar;
        if(ar[pos] == x - i + 1) ar[pos] = inf;
        else
        {
            --pos;
            if(pos == 0) return false;
            else ar[pos] = inf;
        }
        sort(ar + 1, ar + n + 1);
        ar[1] += x - i + 1;
    }
    return true;
}

int main()
{
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; ++i) scanf("%d", &br[i]);

        for(int i = n; i >= 0; --i)
        {
            for(int j = 1; j <= n; ++j) ar[j] = br[j];
            if(judge(i))
            {
                printf("%d\n", i);
                break;
            }
        }

    }


    return 0;
}

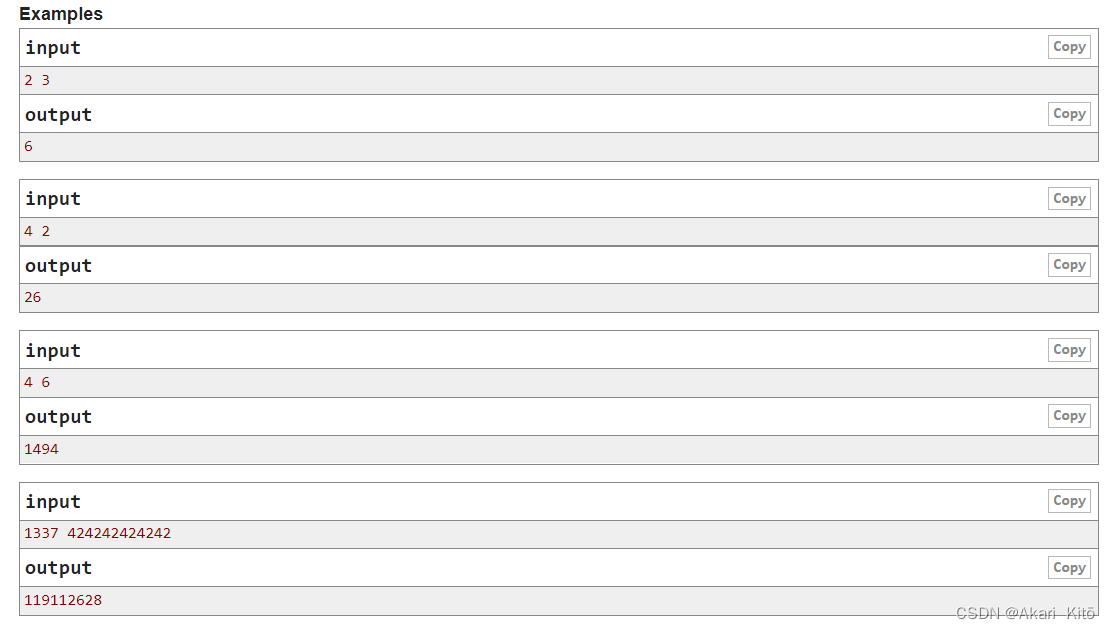
D. Counting Arrays

img

img

题意：
  给出数组是ambiguous的定义：
  对于数组a，如果$gcd(a_i,i) =1$，则可以将$a_i$删除，删除后i右边的数字自动往前填充最终可以将整个数组a删完，数组b记录的是数组a的删除序列，满足$1<=bi<=n-i+1$,$b_i$表示第$i$次删除的数字是$a_{b_i}$(注意在删除的过程中，由于右边的数字会自动向前填充)。如果一个数组a，它的删除序列b不唯一，则认为数组a是ambiguous的。
  输入n，m，数组a中每个元素的取值范围范围是（1~ m),问所有长度1~n的数组中ambiguous的数量的总和是多少。
分析：
  对于任意一个数组，都存在至少一个删除序列b，即所有的$bi=1,$只要数组a存在除了[1,1,…,1]之外的删除序列那么他就是ambiguous的，正向思考情况比较复杂，我们考虑逆向思考，即求所有只能通过[1,1,…,1]删除的序列，然后减去，对于数组a中2 ~ n的任意位置i，如果他只能在移动到1时被删除，则满足$a[i]$是2 ~ i内所有质数的乘积的倍数。那么对于一个不ambiguous的数组a，他的每一位的取值就可确定，之后计算即可。注意运算过程多取模，放溢出。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

const ll mod = 998244353;
ll n, m, ans, num;
ll bas, sub, mul;
const ll maxn = 300005;
bool prime[maxn];
ll Prime[maxn];
ll sum = 0;
bool flag;

void make_prime()
{
    memset(prime, true, sizeof(prime));
    prime[0] = prime[1] = false;
    for(ll i = 2; i <= maxn; i++)
    {
        if(prime[i])
        {
            Prime[num++]=i;
        }
        for(ll j=0; j < num && i * Prime[j] < maxn; j++)
        {
            prime[i * Prime[j]] = false;
            if(!(i % Prime[j]))
                break;
        }
    }
}

int main()
{
    make_prime();

    scanf("%lld%lld", &n, &m);
    //cout << n << ' ' << m << '\n';

    //for(int i = 1; i <= 100; ++i) cout << i << ' ' << prime[i] << '\n';

    bas = m;    //m^n累乘
    sub = m;    //不符合条件的数量
    mul = 1ll;  //2-i内所有质数的乘积
    for(ll i = 2; i <= n; ++i)
    {
        bas = ((bas % mod) * (m % mod)) % mod;
        if(flag)
        {
            ans = (ans + bas) % mod;
            //cout << i << ' '<< mul << ' ' << sub << ' ' << ans << '\n';
            continue;
        }

        if(prime[i]) mul *= i;
        if(mul > m)
        {
            sub = 0;
            flag = true;
        }

        if(flag) ans = (ans + bas) % mod;
        else
        {
            sum = m / mul;
            sub = ((sub % mod) * (sum % mod)) % mod;
            ans = (ans + ((bas - sub) % mod + mod) % mod) % mod;
        }
        //cout << i << ' '<< mul << ' ' << sub << ' ' << ans << '\n';

        //if(i == 50) cout << 555555 << '\n';
    }

    printf("%lld\n", ans);

    return 0;
}

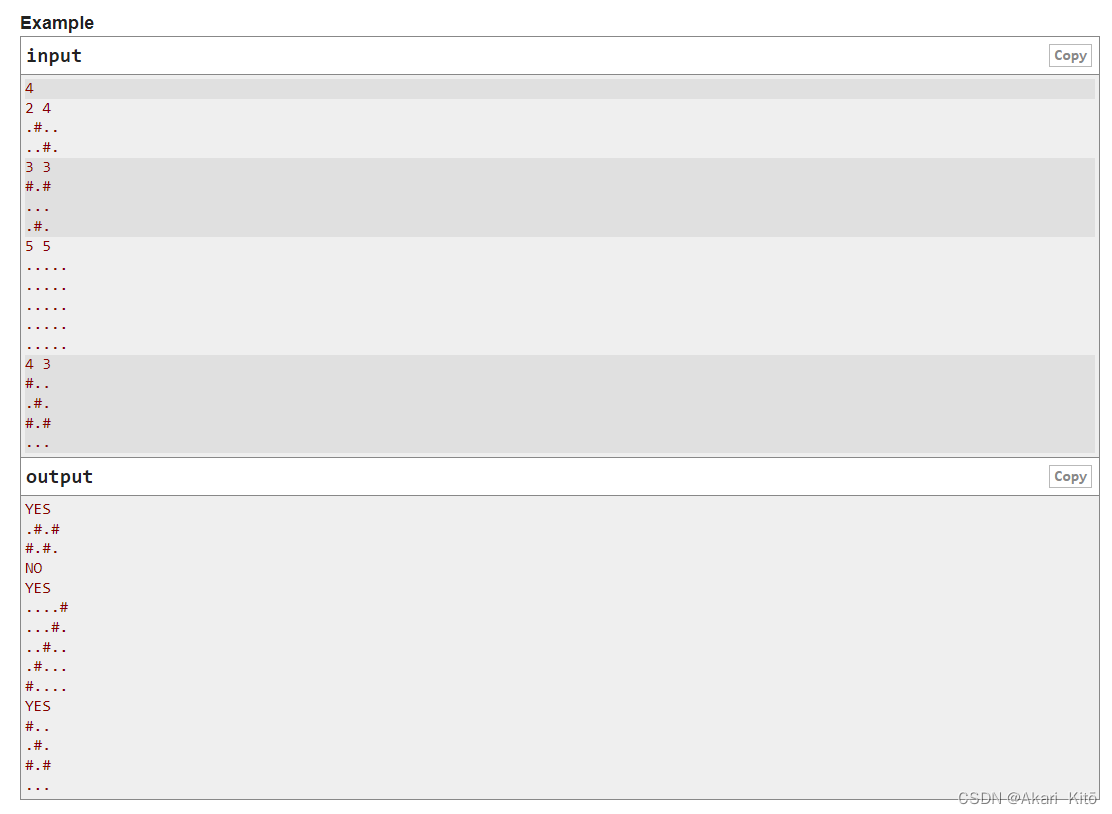
E. Cactus Wall

img

img

题意：
  对于每个样例，给你一张地图，.表示空地，#表示墙，空地可以走，墙不可以。让你修建尽可能少的墙，使得第1行和第n行不连通（第1行的任意一个点不存在任意一条通往第n行任意一个点的路径）。任何一个墙的上下左右不能存在墙，问你有没有一种修法，有输出YES，并将按照任意一种修墙最少的修法后的地图输出，没有输出NO。
分析：
  多源01bfs
  实质就是找一条从最左边一列到最右边一列的路径（这条路径中只能斜着走，左上，左下，右上，右下），就是一条横着的路径，因为要阻挡一条竖着的路径。
  起点是mp[1~n][1],终点是mp[1~n][m]，对于一个点，要走到这个点的话，如果是#那么距离是0，如果是.那么距离是1.
  另外，注意这题的空间，vector的初始化，函数内定义函数（)
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
int t;
int n, m;
string s;
int dx1[4] = {1, -1, 0, 0};
int dy1[4] = {0, 0, 1, -1};
int dx2[4] = {1, 1, -1, -1};
int dy2[4] = {1, -1, 1, -1};
int x, y, nx, ny;

void solve()
{
    scanf("%d%d", &n, &m);

    vector<string> g(n + 5);
    vector<vector<int> > dp(n + 5, vector<int>(m + 1, -1));

    g[0] = string(m + 1, '?');
    g[n + 1] = string(m + 1, '?');

    for(int i = 1; i <= n; ++i)
    {
        cin >> s;
        g[i] = "?" + s;
    }

    auto judge = [&](int x, int y)
    {
        if(x <= 0 || x > n || y <= 0 || y > m) return false;
        for(int i = 0; i < 4; ++i)
        {
            if(g[x + dx1[i]][y + dy1[i]] == '#') return false;
        }
        return true;
    };

    deque<pair<int, int> > q;
    for(int i = 1; i <= n; ++i)
    {
        if(g[i][1] == '#')
        {
            dp[i][1] = 0;
            q.push_front({i, 1});
        }
        else
        {
            if(judge(i, 1))
            {
                dp[i][1] = 1;
                q.push_back({i, 1});
            }
        }
    }

    map<pair<int,int>, pair<int, int>> pre;
    while(!q.empty())
    {
        x = q.front().first, y = q.front().second;
        q.pop_front();

        for(int i = 0; i < 4; ++i)
        {
            nx = x + dx2[i];
            ny = y + dy2[i];
            if(!judge(nx, ny)) continue;

            if(dp[nx][ny] != -1) continue;
            if(g[nx][ny] == '#')
            {
                dp[nx][ny] = dp[x][y];
                pre[{nx, ny}] = {x, y};
                q.push_front({nx, ny});
            }
            else
            {
                dp[nx][ny] = dp[x][y] + 1;
                pre[{nx, ny}] = {x, y};
                q.push_back({nx, ny});
            }
        }
    }

    int mi = inf;
    pair<int, int> pi;
    for(int i = 1; i <= n; ++i)
    {
        if(dp[i][m] != -1 && dp[i][m] < mi)
        {
            mi = dp[i][m];
            pi = {i, m};
        }
    }

    if(mi == inf)
    {
        printf("NO\n");
        return ;
    }

    printf("YES\n");

    g[pi.first][pi.second] = '#';
    while(pre.count(pi))
    {
        pi = pre[pi];
        g[pi.first][pi.second] = '#';
    }

    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= m; ++j) putchar(g[i][j]);
        putchar('\n');
    }
}

int main()
{
    scanf("%d", &t);

    while(t--) solve();

    return 0;
}