Codeforces Round#826 (Div. 3) D E F

发表于 更新于 分类于

Codeforces Round #826 (Div. 3) D E F

D. 递归
E. 递推/简单DP
F. 排序+维护前缀最大值和次大值

D. Masha and a Beautiful Tree (递归)

img
img
img
img
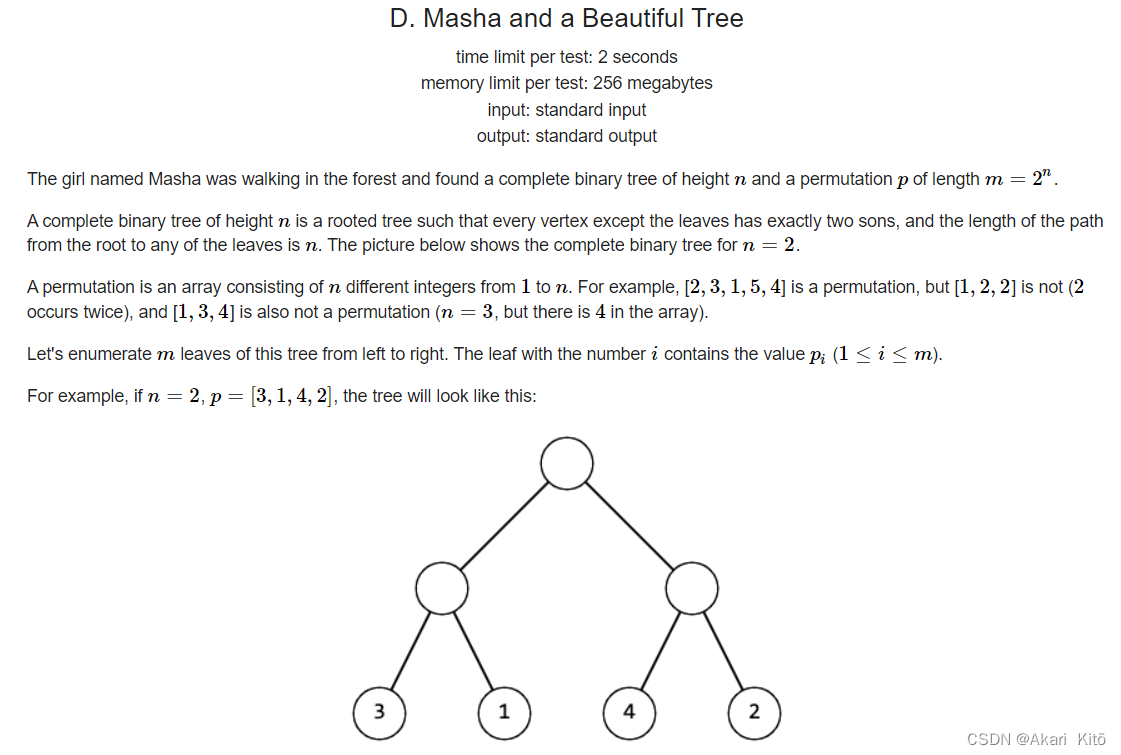
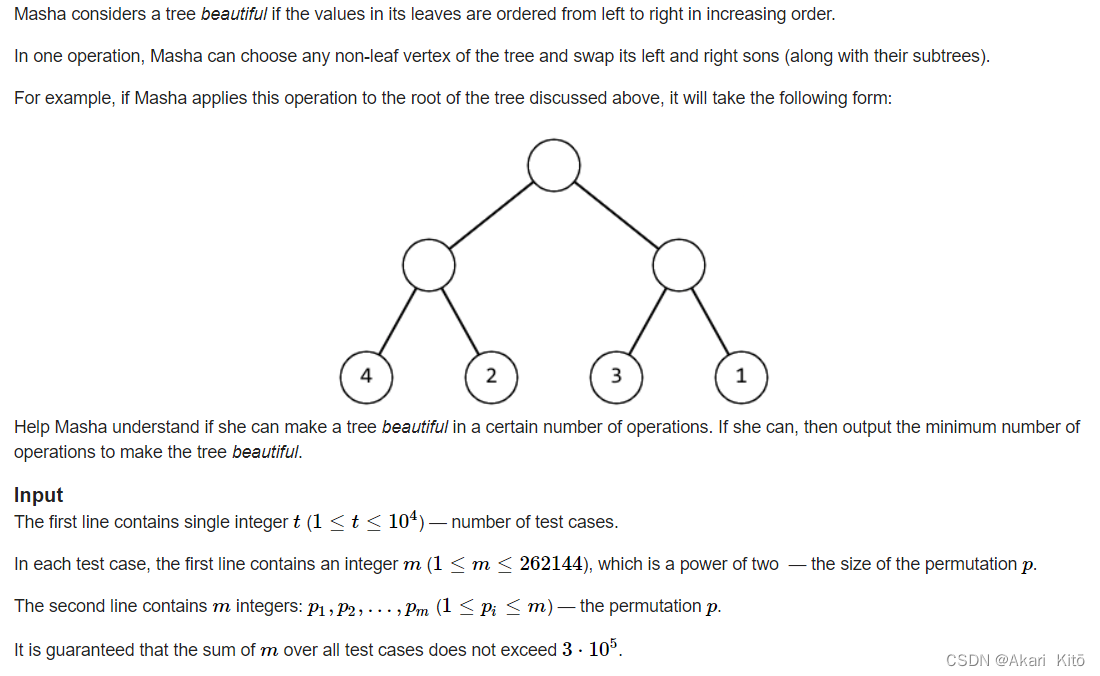
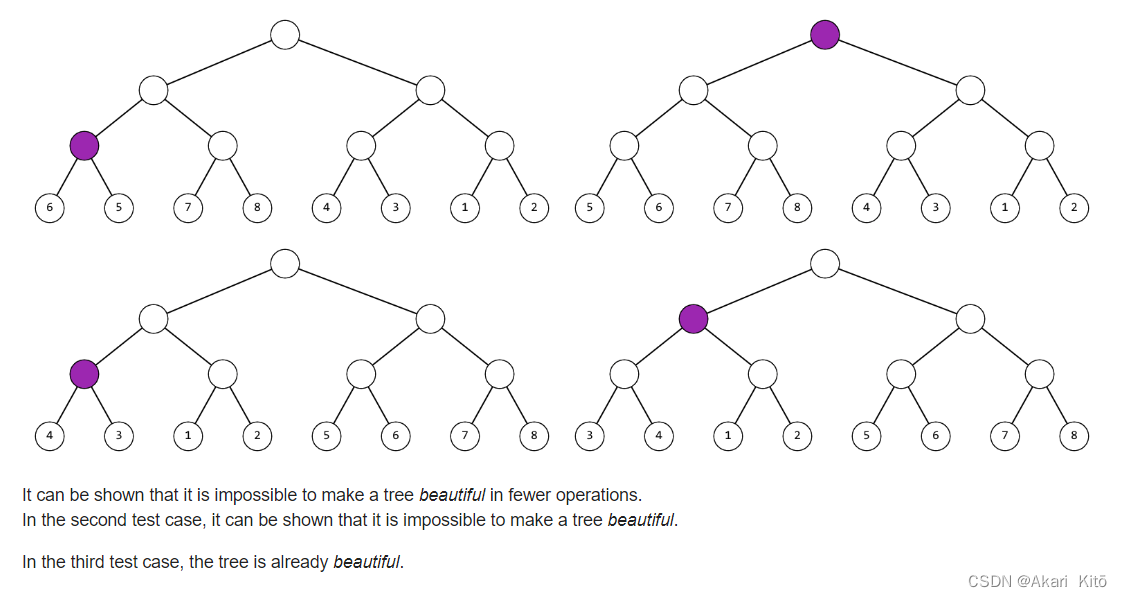
题意：
  对于每个样例，输入一个m，之后输入一个长度为m的排列（m好像保证一定是2^i），输入的排列是一颗完全二叉树的叶子结点。你可以进行一种操作：操作每一个非叶子节点，交换他的两个左右儿子（左右子树也会跟着交换）。问你进行多少次操作可以使这个排列p满足$p_i = i$，输出最小的操作次数，无法操作输出-1。
分析：
  二叉树是递归定义的。
  可以考虑把这棵树看成一颗线段树，维护区间最大值（或者最小值），这样每个结点的值就都有了，我们假设叶子结点所在那层为第0层，其父亲结点在第1层，。。。，根节点在最高层，那么对于第i层的两个兄弟结点$p_1, p_2$，它们必须满足$|p_1 - p_2| = 2^i$，否则答案将是-1。对于操作，如果左儿子大于右儿子，则需要操作其父节点。二叉树是递归定义的，递归跑一遍即可（dfs)。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>

using namespace std;

int t, n;
int ar[300000];
bool flag;
int ans;
int bas[30];

struct node
{
    int l, r, mi;
    int dep;
}tree[1100050];

void init()
{
    bas[0] = 1;
    for(int i = 1; i <= 30; ++i) bas[i] = bas[i - 1] * 2;
}

void pushup(int p)
{
    if(abs(tree[p<<1].mi - tree[p<<1|1].mi) != bas[tree[p<<1].dep]) flag = true;
    tree[p].mi = min(tree[p<<1].mi, tree[p<<1|1].mi);
}

void build(int p, int l, int r)
{
    tree[p].l = l, tree[p].r = r;

    if(l == r)
    {
        tree[p].mi = ar[l];
        tree[p].dep = 0;
        return ;
    }

    int mid = (l + r) >> 1;

    build(p<<1, l, mid);
    build(p<<1|1, mid + 1, r);
    tree[p].dep = tree[p<<1].dep + 1;

    pushup(p);
}

void dfs(int p)
{
    if(tree[p].l == tree[p].r) return;

    if(tree[p<<1].mi > tree[p<<1|1].mi) ++ans;
    dfs(p<<1);
    dfs(p<<1|1);
}

int main()
{
    scanf("%d", &t);

    init();

    while(t--)
    {
        scanf("%d", &n);

        for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

        flag = false;
        ans = 0;

        build(1, 1, n);
        if(flag)
        {
            printf("-1\n");
            continue;
        }

        dfs(1);

        printf("%d\n", ans);
    }
    return 0;
}

E. Sending a Sequence Over the Network（递推/简单dp）

img
img
img
题意：
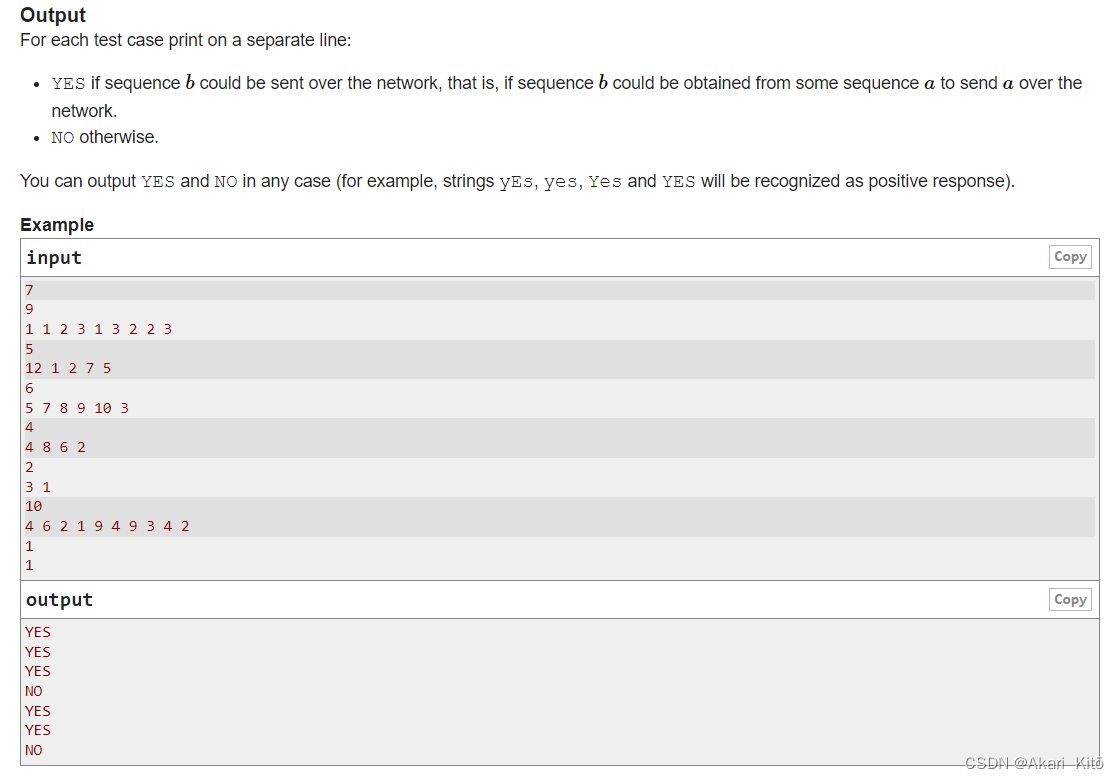
  对于一个长度为m的数组ar，可以将它分割成很多段（$l_i,r_i$），任意一段没有交集，且所有段合起来是（1，n）之后在某一段的左边或者右边添加一个数字k，k为这一段的长度，由此获得数组br。
  对于每一个样例，输入一个n，代表数组br的长度，之后输入数组br，问是否存在一个数组ar，经过操作后能够变成数组br。
分析：
  定义一个bool类型数组vis，vis[i]表示数组br中，位置i能否作为一段的终止，$O(n)$递推转移一下即可（对于每个点，枚举他作为区间最左或者最右的情况)，注意不要re，答案就是vis[n]。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>

using namespace std;

bool vis[200050];
int t, n;
int ar[200050];

int main()
{
    scanf("%d", &t);

    while(t--)
    {
        scanf("%d", &n);

        for(int i = 1; i <= n; ++i)
        {
            scanf("%d", &ar[i]);
            vis[i] = false;
        }

        vis[0] = true;
        for(int i = 1; i <= n; ++i)
        {
            if(i - ar[i] - 1 >= 0) vis[i] |= vis[i - ar[i] - 1];

            if(i + ar[i] <= n) vis[i + ar[i]] |= vis[i - 1];
        }

        if(vis[n]) printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

F. Multi-Colored Segments （排序+维护前缀最大值和前缀次大值）

img
img
img
img
img
img
题意：
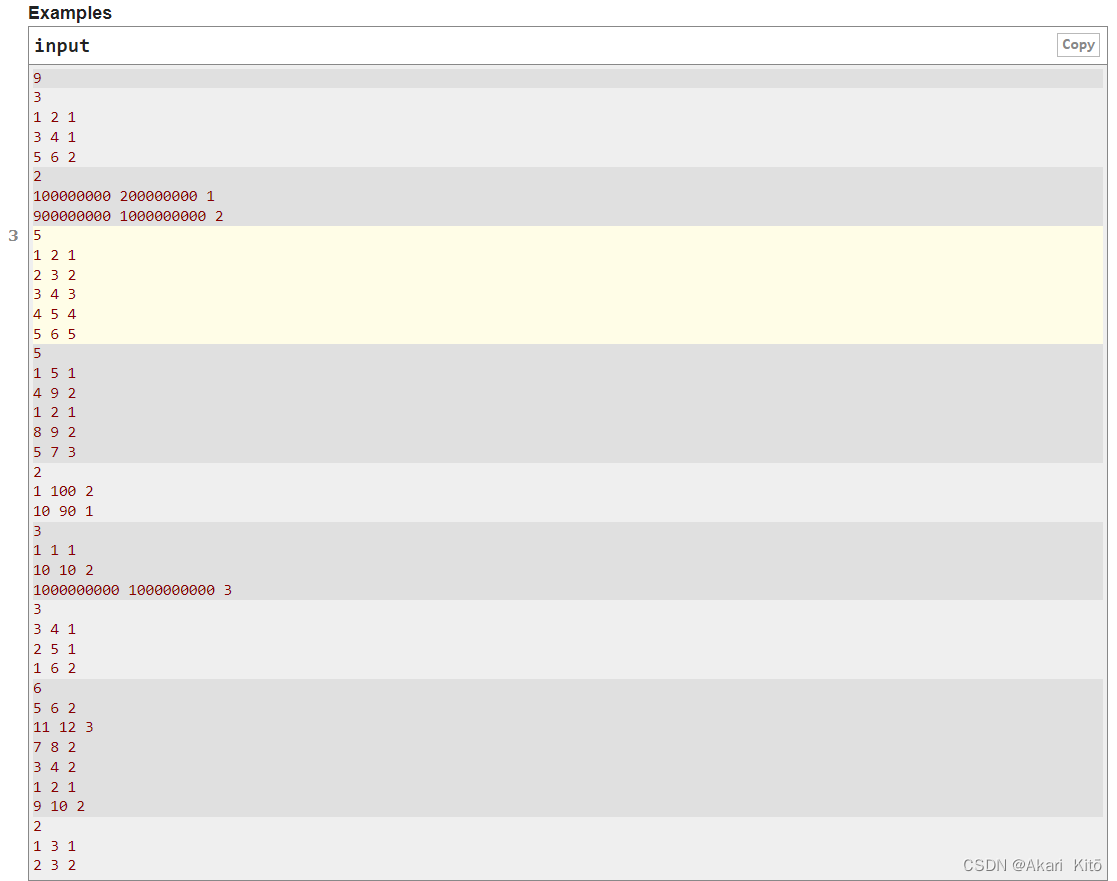
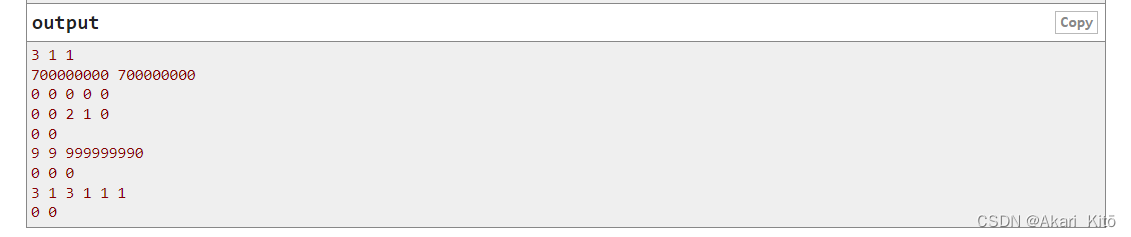
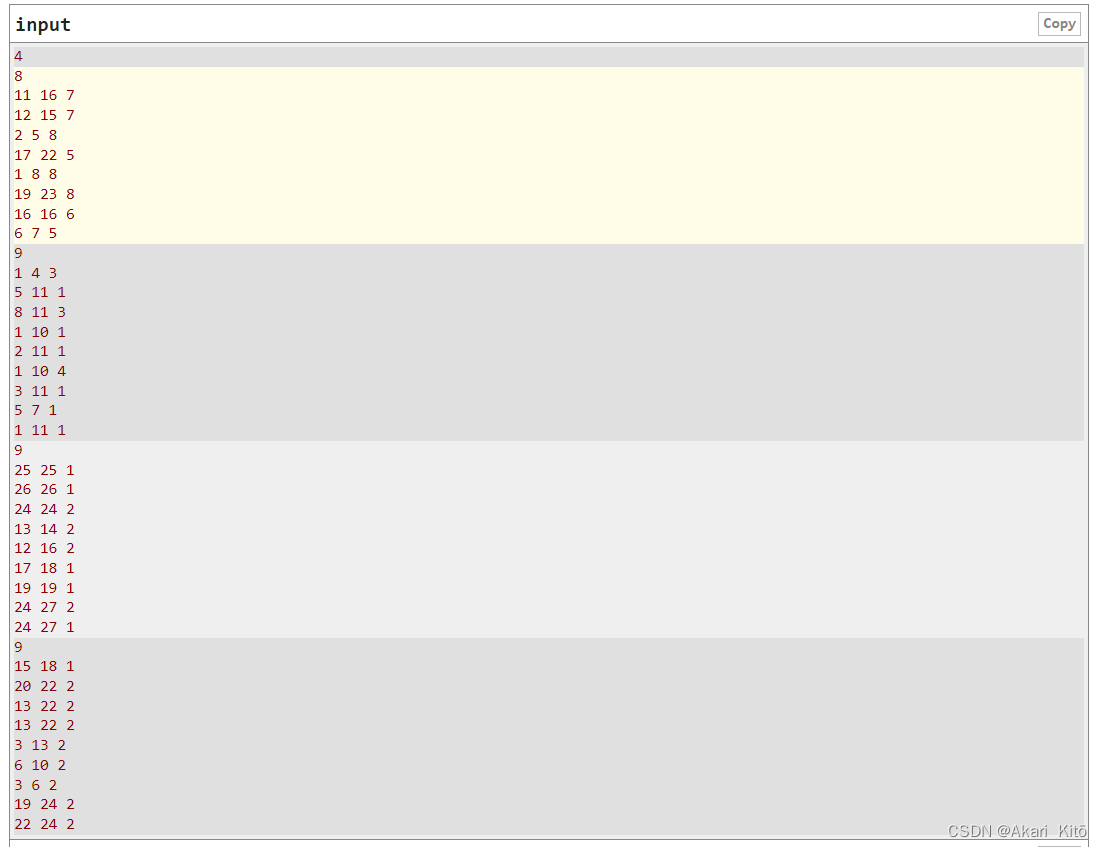
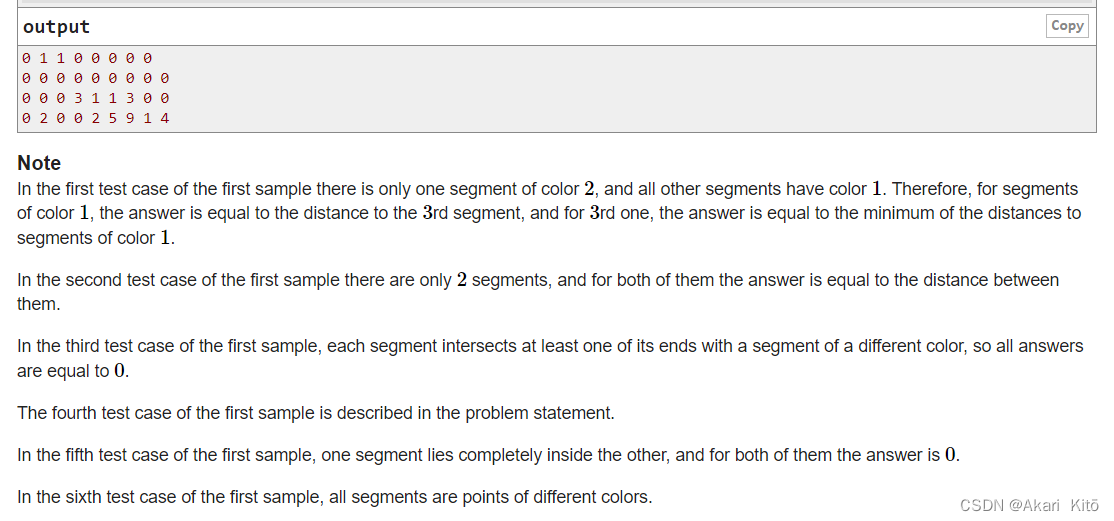
  在一个数轴上有n个线段，对于每段线段，其左端点和右端点一定是整数，每个线段有一个颜色，两个线段的距离是从两个线段中分别选取两个点求两点间距离，这个距离的最小值为两个线段的距离（相交距离为0，不相交左面线段选右端点，右面线段选左端点）。对于每段线段，求离它最近的一个和它颜色不同的线段的距离。
分析：
  对于线段$i$$(l_i,r_i,c_i)$，离它最近的且和它颜色不同的线段的距离可以分为两部分，位于$r_i$左侧的线段（如果线段$j$满足$l_j<=r_i$，则认为线段$j$位于其左侧）且于线段$i$颜色不同的线段距线段$i$的距离$s_1$，位于$l_i$右侧的且于线段$i$颜色不同的线段距线段$i$的距离为$s_2$，则$ans_i = min(s_1, s_2)$.
对于某个线段$i$,求其$s_1$,维护满足条件的线段$j$的$r_j$的最大值和次大值（最大值和次大值对应的线段颜色应当不同，即一种颜色只记一个最大值），若线段$i$与最大值对应线段颜色不同，则$s_1$由最大值决定(假设最大值是$mx$，则$s_1 = max(0,mx-r_i)$)，否则由次大值决定。
  由此，可通过排序+遍历取得，对于求$s_i$应将线段$i$所在数组按照$r_i$从小到大排序，线段$j$所在的数组按照$l_j$从小到大排序，之后遍历即可。而对于$s_2$，可以将线段的 $l=l\times(-1)$，$r=r\times(-1)$之后$swap(l,r)$，再按照上面求$s_1$的方法计算一遍即可得$s_2$ 。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
int t, n;
int mxl[200050], mxr[200050];//两次遍历过程中颜色i对应线段的最大值
struct node
{
    int l, r, c;
    int id;
} ar[200050], br[200050];
int mx_l, mxl_color, mxxl, mxxl_color;//第一次遍历过程中的最大值，最大值对应的颜色，次大值
int mx_r, mxr_color, mxxr, mxxr_color;
int ans[200050];
bool flag1, flag2;//是否有最大值，次大值

bool cmp1(node a, node b)
{
    return a.r < b.r;
}

bool cmp2(node a, node b)
{
    return a.l < b.l;
}

void init()
{
    mx_l = mxl_color = mxxl = mxr_color = 0;
    mx_r = mxxr = -inf;
    flag1 = flag2 = false;
    for(int i = 1; i <= n; ++i)
    {
        mxl[i] = 0;
        ans[i] = inf;
        mxr[i] = -inf;
    }
}

void work_l()
{
    int beg = 0, color = 0;
    for(int i = 1; i <= n; ++i)
    {
        //cout << i << '\n';
        for(int j = beg + 1; br[j].l <= ar[i].r && j <= n; ++j)
        {
            //cout << j << '\n';
            color = br[j].c;
            if(br[j].r > mxl[color])
            {
                mxl[color] = br[j].r;
                if(mxl[color] > mx_l)
                {
                    if(mxl_color == color) mx_l = mxl[color];
                    else
                    {
                        mxxl = mx_l;
                        mx_l = mxl[color];
                        mxl_color = color;
                        flag1 = true;
                        if(mxxl != 0) flag2 = true;
                    }
                }
                else if(mxl[color] > mxxl && color != mxl_color)
                {
                    mxxl = mxl[color];
                    flag2 = true;
                }
            }
            beg = j;
        }

        //cout << i << ' ' << beg << '\n';

        //cout << i << ' ' << flag1 << ' ' << flag2 << '\n';
        if(ar[i].c != mxl_color && flag1) ans[ar[i].id] = min(ans[ar[i].id], max(0, ar[i].l - mx_l));
        else if(flag2) ans[ar[i].id] = min(ans[ar[i].id], max(0, ar[i].l - mxxl));
    }
}

void work_r()
{
    int beg = 0, color = 0;
    for(int i = 1; i <= n; ++i)
    {
        for(int j = beg + 1; br[j].l <= ar[i].r && j <= n ; ++j)
        {
            //cout << br[j].id << '\n';
            color = br[j].c;
            if(br[j].r > mxr[color])
            {
                mxr[color] = br[j].r;
                if(mxr[color] > mx_r)
                {
                    if(mxr_color == color) mx_r = mxr[color];
                    else
                    {
                        mxxr = mx_r;
                        mx_r = mxr[color];
                        mxr_color = color;
                        flag1 = true;
                        if(mxxr != -inf) flag2 = true;
                    }

                }
                else if(mxr[color] > mxxr && color != mxr_color)
                {
                    mxxr = mxr[color];
                    flag2 = true;
                }
            }
            beg = j;
        }
        if(ar[i].c != mxr_color && flag1) ans[ar[i].id] = min(ans[ar[i].id], max(0, ar[i].l - mx_r));
        else if(flag2) ans[ar[i].id] = min(ans[ar[i].id], max(0, ar[i].l - mxxr));
    }
}

int main()
{
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; ++i)
        {
            scanf("%d%d%d", &ar[i].l, &ar[i].r, &ar[i].c);
            ar[i].id = i;
            br[i] = ar[i];
        }

        //cout << 1 << '\n';

        sort(ar + 1, ar + n + 1, cmp1);
        sort(br + 1, br + n + 1, cmp2);

//        for(int i = 1; i <= n; ++i) cout << i << ' ' << ar[i].l << ' ' << ar[i].r << ' ' << ar[i].id << '\n';
//        for(int i = 1; i <= n; ++i) cout << i << ' ' << br[i].l << ' ' << br[i].r << ' ' << br[i].id << '\n';

        init();

        //cout << 2 << '\n';

        work_l();

//        for(int i = 1; i <= n; ++i) printf("%d ", ans[i]);
//        putchar('\n');

        //cout << 3 << '\n';

        for(int i = 1; i <= n; ++i)
        {
            ar[i].l *= -1, ar[i].r *= -1;
            swap(ar[i].l, ar[i].r);
            br[i].l *= -1, br[i].r *= -1;
            swap(br[i].l, br[i].r);
        }

        sort(ar + 1, ar + n + 1, cmp1);
        sort(br + 1, br + n + 1, cmp2);
        flag1 = flag2 = false;

//        for(int i = 1; i <= n; ++i) cout << i << ' ' << ar[i].l << ' ' << ar[i].r << ' ' << ar[i].id << '\n';
//        for(int i = 1; i <= n; ++i) cout << i << ' ' << br[i].l << ' ' << br[i].r << ' ' << br[i].id << '\n';

        //cout << 4 << '\n';

        work_r();

        //cout << 5 << '\n';

        for(int i = 1; i <= n; ++i) printf("%d ", ans[i]);
        putchar('\n');

    }
    return 0;
}