主席树 洛谷P3834&POJ2104&HDU 6278

发表于 更新于 分类于

主席树

主席树模板

P3834 【模板】可持久化线段树 2（主席树）（洛谷）

POJ2104

img
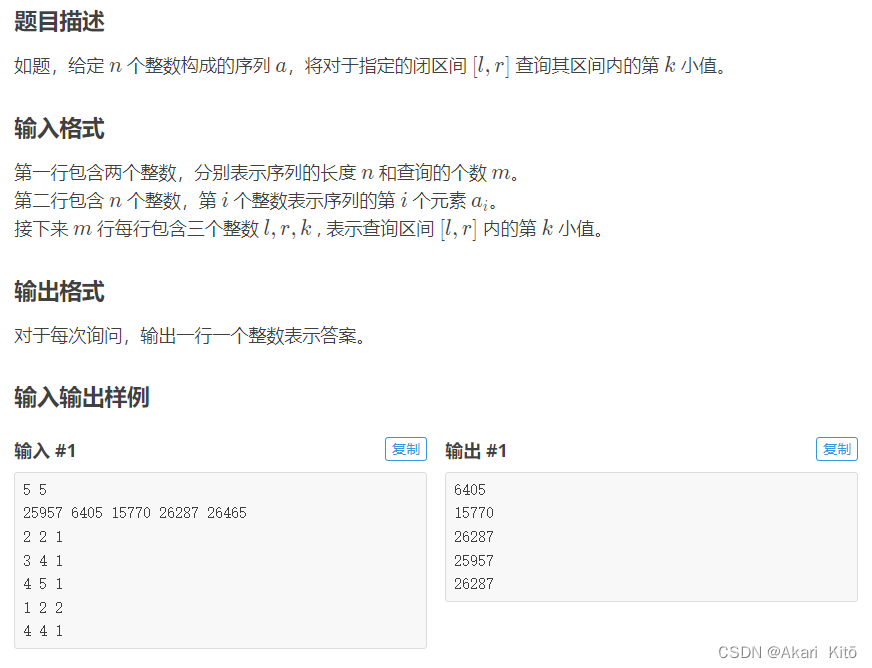
题意：
两道题都是求区间第k小
分析：
1.预处理原数组，排序，去重，离散化（用普通数组即可离散化，不习惯用vector）
2.建树，与普通线段树不同在于，线段树是把一坨数输进来之后直接build（1，1，n）即可，主席树是一个一个点的修改，即维护不同版本的权值线段树。
对于新一个版本的权值线段树，都会先添加一个根节点作为当前版本的根节点，也是便于后续查询某个版本的权值线段树，然后把上一个版本的权值线段树复制给当前版本（当前根节点 = 上一个版本根节点)，然后进行修改，两个版本权值线段树不同就在于新增加的这一个元素，不同的结点即根节点到新增结点路径上的所有结点，这些结点是需要新增加的，把这些结点放在新版本根节点之下，新版本的其他点也上一个版本相同，由此我们可以发现对于一个点，他可能有多个父亲，故对于主席树来说，找父亲儿子不能简单的通过/2或*2解决，我们需要存每个结点的左右儿子。

1
2
3
4
5
6
7
8
9
10
11
12
13
//l，r区间边界，pre上一个版本的根（父）结点，now当前版本的根（父）节点，p需要修改的值（由于离散化，p值多1，即第p个大）
void updata(int l, int r, int pre, int &now, int p)
{
    tree[++cnt] = tree[pre];//给新版本根（父）节点一个空间，并复制上一个版本的根（父）节点给它
    now = cnt;//改变当前版本根（父）结点的编号
    ++tree[now].sum;//由于新加了一个元素，当前版本元素总数加1
    //递归修改（新建）根节点到新的点路径上的所有点
    if(l == r) return ;//找到这个点return即可
    //判断需要向左儿子改还是向右儿子改
    mid = (l + r) >> 1;
    if(p <= mid) updata(l, mid, tree[pre].l, tree[now].l, p);
    else updata(mid + 1, r, tree[pre].r, tree[now].r, p);
}

3.查询操作

1
2
3
4
5
6
7
8
9
10
11
//查询区间L + 1到R的第k小的值
int query(int l, int r, int L, int R, int k)
{
    if(l == r) return l;//递归到叶子结点，return 即可
    mid = (l + r) >> 1;
    tmp = tree[tree[R].l].sum - tree[tree[L].l].sum;
    //求出R版本的权值线段树与L版本的权值线段树左子树差多少个树，左子树的数一定小于右子树
    //tmp值即第1~tmp小的值在左子树，再根据tmp值与k值的关系向左/右子树递归。
    if(k <= tmp) return query(l, mid, tree[L].l, tree[R].l, k);
    else return query(mid + 1, r, tree[L].r, tree[R].r, k - tmp);
}

需要维护的容器&变量

1
2
3
4
5
6
7
8
1.struct node
{
    int l, r, sum;
}tree[maxn*30]; 
存主席树，*30，40，50的都有。。。据上面的分析易知这个数组的类型是个结构体，存三个量，该点的左右儿子l/r，该点包含区间中元素个数sum
2.root[maxn]  存第i版本的根节点在tree[maxn]数组的下标
3.cnt  用于更新主席树时，新加结点的分配。
4.br[maxn]  原数组离散化后的数组

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>

using namespace std;

const int maxn = (int)2e5 + 5;
int n, m, l, r, k;
int mid, id, tmp;
int cnt, en;
int ar[maxn];
int br[maxn];
struct node
{
    int l, r, sum;
}tree[maxn*30];
int root[maxn];

inline int read()
{   char ch = getchar();int s = 0, w = 1;
    while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}
    return s * w;
}

void updata(int l, int r, int pre, int &now, int p)
{
    tree[++cnt] = tree[pre];
    now = cnt;
    ++tree[now].sum;
    if(l == r) return ;
    mid = (l + r) >> 1;
    if(p <= mid) updata(l, mid, tree[pre].l, tree[now].l, p);
    else updata(mid + 1, r, tree[pre].r, tree[now].r, p);
}

int query(int l, int r, int L, int R, int k)
{
    if(l == r) return l;
    mid = (l + r) >> 1;
    tmp = tree[tree[R].l].sum - tree[tree[L].l].sum;
    if(k <= tmp) return query(l, mid, tree[L].l, tree[R].l, k);
    else return query(mid + 1, r, tree[L].r, tree[R].r, k - tmp);
}

int main()
{
    n = read(); m = read();
    for(int i = 1; i <= n; ++i)
    {
        ar[i] = read();
        br[i - 1] = ar[i];
    }
    sort(br, br + n);
    en = unique(br, br + n) - br;
    for(int i = 1; i <= n; ++i)
    {
        id = lower_bound(br, br + en, ar[i]) - br + 1;
        updata(1, n, root[i - 1], root[i], id);
    }
    while(m--)
    {
        l = read(); r = read(); k = read();
        printf("%d\n", br[query(1, n, root[l - 1], root[r], k) - 1]);
    }
    return 0;
}

HDU 6278

分析：
需要求的是区间最h大值，二分答案判区间第h大的值是否大于等于h即可
求第h大的值，查询函数需要稍微修改一下，tmp值应该是两个版本右子树sum值相减。。。
AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <cstdio>
#include <algorithm>
#include <iostream>

using namespace std;

const int maxn = (int)2e5 + 5;
int n, m, l, r, k;
int mid, id, tmp;
int cnt, en;
int st, enn;
int ar[maxn];
int br[maxn];
struct node
{
    int l, r, sum;
}tree[maxn*30];
int root[maxn];

inline int read()
{   char ch = getchar();int s = 0, w = 1;
    while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}
    return s * w;
}

void updata(int l, int r, int pre, int &now, int p)
{
    tree[++cnt] = tree[pre];
    now = cnt;
    ++tree[now].sum;
    if(l == r) return ;
    mid = (l + r) >> 1;
    if(p <= mid) updata(l, mid, tree[pre].l, tree[now].l, p);
    else updata(mid + 1, r, tree[pre].r, tree[now].r, p);
}

int query(int l, int r, int L, int R, int k)
{
    if(l == r) return l;
    mid = (l + r) >> 1;
    tmp = tree[tree[R].r].sum - tree[tree[L].r].sum;
    if(tmp >= k) return query(mid + 1, r, tree[L].r, tree[R].r, k);
    else return query(l, mid, tree[L].l, tree[R].l, k - tmp);
}

bool judge(int x)
{
    if(br[query(1, n, root[st - 1], root[enn], x) - 1] >= x) return true;
    else return false;
}

int main()
{
    while(~scanf("%d%d", &n, &m))
    {
        cnt = 0;
        for(int i = 1; i <= n; ++i)
        {
            ar[i] = read();
            br[i - 1] = ar[i];
        }
        sort(br, br + n);
        en = unique(br, br + n) - br;
        for(int i = 1; i <= n; ++i)
        {
            id = lower_bound(br, br + en, ar[i]) - br + 1;
            updata(1, n, root[i - 1], root[i], id);
        }
        while(m--)
        {
            st = read(); enn = read();
            l = 0; r = enn - st + 1;
            //cout << l << ' ' << r << endl;
            while(l <= r)
            {
                int midd = (l + r) >> 1;
                //cout << mid << endl;
                if(judge(midd)) l = midd + 1;//cout << mid << ' ' ;}
                else r = midd - 1;
            }
            printf("%d\n", l - 1);
        }
    }
    return 0;
}

这个题一开始出现了一扭扭错误，因为习惯把所有能用到的变量定义在全局，这样可以避免跑循环是一直定义变量，但这样二分答案时和query查询时，两个函数里都有mid，然后二分退出来的时候就不是一开始传进去的mid了。。。无奈又改了变量名。。。